题目内容
【题目】由某种金属材料制成的圆柱形导体,将其两端与电源连接,会在导体内部形成匀强电场,金属中的自由电子会在电场力作用下发生定向移动形成电流。已知电子质量为m,电荷量为e,该金属单位体积的自由电子数为n。
(1)若电源电动势为E,且内阻不计,
a. 求电源从正极每搬运一个自由电子到达负极过程中非静电力所做的功W非;
b. 从能量转化与守恒的角度推导:导体两端的电压U等于电源的电动势E;
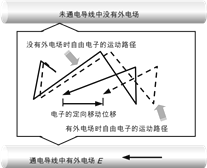
(2)经典的金属电子论认为:在外电场(由电源提供的电场)中,金属中的自由电子受到电场力的驱动,在原热运动基础上叠加定向移动,如图所示。在定向加速运动中,自由电子与金属正离子发生碰撞,自身停顿一下,将定向移动所获得的能量转移给金属正离子,引起正离子振动加剧,金属温度升高。自由电子在定向移动时由于被频繁碰撞受到阻碍作用,这就是电阻形成的原因。
自由电子定向移动的平均速率为v,热运动的平均速率为u,发生两次碰撞之间的平均距离为x。由于v<<u,所以自由电子发生两次碰撞的时间间隔主要由热运动决定。自由电子每次碰撞后的定向移动速率均变为零。
a. 求该金属的电阻率ρ,并结合计算结果至少说明一个与金属电阻率有关的宏观因素;
b. 该导体长度为L,截面积为S。若将单位时间内导体中所有自由电子因与正离子碰撞而损失的动能之和设为ΔEk,导体的发热功率设为P,试证明P=ΔEk。
【答案】(1)a.![]() ;b.见解析(2)a. 从计算结果可知,金属的电阻率与金属中单位体积的自由电子数n、自由电子热运动平均速率u和碰撞的平均距离x有关,所以在宏观上,电阻率与金属的种类和温度有关;b.见解析
;b.见解析(2)a. 从计算结果可知,金属的电阻率与金属中单位体积的自由电子数n、自由电子热运动平均速率u和碰撞的平均距离x有关,所以在宏观上,电阻率与金属的种类和温度有关;b.见解析
【解析】(1)a.由![]() 可知,
可知,![]() ;
;
b. 由能量转化与守恒定律可知,电场力做功等于非静电力做功,即![]() ;
;
设电路中的电流为I,则在t时间内![]()
所以有![]() ,即
,即![]() ;
;
(2)a. 设导体长度为L,截面积为S,两端电压为U,通过的电流为I。
电子发生两次碰撞之间,在原有的匀速运动(热运动)的同时,叠加在外电场作用下由静止开始的匀加速运动(定向移动),但因![]() ,
,
所以两次碰撞的平均时间间隔![]() ,
,
电子在外电场中做定向移动的加速度![]() ,
,
电子碰撞前瞬间的定向移动速度![]() ,且
,且![]() ,
,
整理可得导体两端电压![]() ;
;
设在Δt时间内流过导体的电荷量![]() ;
;
由![]() 可知:
可知:![]() ,代入
,代入![]() ,
,
与电阻定律![]() 比较,有
比较,有![]() ;
;
从计算结果可知,金属的电阻率与金属中单位体积的自由电子数n、自由电子热运动平均速率u和碰撞的平均距离x有关,所以在宏观上,电阻率与金属的种类和温度有关。(只要说出一种因素即可得分)
b. 导体的发热功率![]() ;
;
单位时间内一个自由电子因与正离子碰撞而损失的动能![]()
导体中所有自由电子在单位时间内损失的动能之和![]()
所以![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案