题目内容
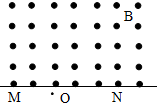如图所示直线MN上方有磁感应强度为B的匀强磁场，方向垂直纸面向外，正、负电子同时从同一点O以与MN成30°角的同样速度v射入磁场（电子质量为m，电荷量为e），它们从磁场中射出时相距分析：粒子做匀速圆周运动，由洛仑兹力充当向心力可知两粒子离开磁场时的距离，则可求出出射点的距离；根据两粒子在磁场中转动的时间可知时间差．
解答：解：正、负电子在磁场中的回旋轨迹如图所示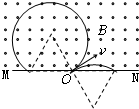
由evB=
得
R=
T=
∵θ=300
如图可知，两粒子离开时距O点均为R，
所以出射点相距为L=2R=
；
正电子的回旋时间为 t1=
=
负电子的回旋时间为t2=
T=
射出的时间差为△t=t2-t1=
故答案：
，
由evB=
| mv2 |
| R |
R=
| mv |
| eB |
T=
| 2πm |
| eB |
∵θ=300
如图可知，两粒子离开时距O点均为R，
所以出射点相距为L=2R=
| 2mv |
| eB |
正电子的回旋时间为 t1=
| T |
| 6 |
| πm |
| 3eB |
负电子的回旋时间为t2=
| 5 |
| 6 |
| 5πm |
| 3eB |
射出的时间差为△t=t2-t1=
| 4πm |
| 3eB |
故答案：
| 2mv |
| eB |
| 4πm |
| 3eB |
点评：带电粒子在电场中的运动关键在于由几何关系找出圆心和半径，再由洛仑兹力充当向心力及圆的性质可得出几何关系及转动时间．
练习册系列答案
相关题目
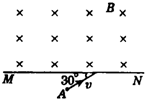如图所示，直线MN上方存在垂直纸面向内、磁感应强度大小为B的匀强磁场，现有一质量为m、带电量为+q的粒子在纸面内以速度v从A点射入，其方向与MN成30°角，A点与直线MN的距离为d，带电粒子重力不计．试求当v满足什么条件时，粒子能回到A．
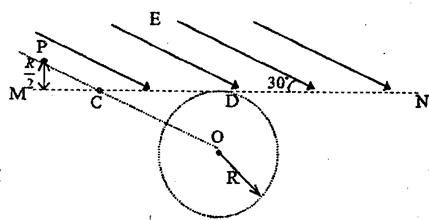如图所示，在水平面直线MN的上方有一方向与MN成30°角的斜向右下方的匀强电场，电场区域足够宽，场强大小为E．在MN下方有一半径为R的圆形区域，圆心为O，圆O与MN相切于D点，圆形区域内分布有垂直纸面向里的匀强磁场．在MN上有一点C，圆心O与C点的连线和电场线平行，在OC的延长线上有一点P，P点到边界MN的垂直距离为0.5R．一质量为m、电荷量为q的带正电的粒子从P点静止释放．已知圆形磁场的磁感应强度大小为
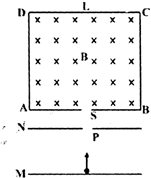如图所示，M，N为水平放置的平行金属板，板间电压为U，在N板中心处有一小孔P，在N板上方有一边长L=1．Om的非磁性正方形绝缘框ABCD，AB边中点处有一小孔S，P和S处于同一竖直线上，绝缘框内有磁感应强度大小B=2T、方向垂直纸面向里的匀强磁场．一质量m=2.0×10-4kg、电荷量g=+5．Ox 10-3c的带电粒子从紧靠M板处静止释放，并从小孔S垂直于AB边射入磁场，粒子和框壁碰撞过程中无动能损失，且碰撞时间可以忽略，不计粒子重力，求：