题目内容
水平台球桌面上母球A、目标球B和球袋洞口边缘C位于一条直线上,设A、B两球质量均为0.25kg且可视为质点,A、B间的距离为5cm,B、C间距离为x=160cm,因两球相距很近,为避免“推杆”犯规(球杆推着两球一起运动的现象),常采用“点杆”击球法(当球杆杆头接触母球的瞬间,迅速将杆抽回,母球在离杆后与目标球发生对心正碰,因碰撞时间极短,可视为完全弹性碰撞),设球与桌面的动摩擦因数为μ=0.5,为使目标球可能落入袋中,求:
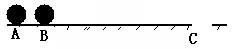
①碰撞过程中A球对B球的最小冲量为多大(碰撞过程中的摩擦阻力可忽略不计)
②碰撞前瞬间A球的速度最小是多大
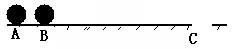
①碰撞过程中A球对B球的最小冲量为多大(碰撞过程中的摩擦阻力可忽略不计)
②碰撞前瞬间A球的速度最小是多大
1kg·m/s 4m/s
试题分析:①设碰撞后瞬间B球能进入球袋的最小速度为vB,由动能定理得:
μmgx=0-=
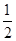 mvB2 解得vB="4m/s" (2分)
mvB2 解得vB="4m/s" (2分)由动量定理得:I=mvB=1kg·m/s (2分)
②设A碰撞前瞬间最小速度为vA,碰撞后瞬间为v,则:
由动量守恒定律得:mvA=mv+mvB (2分)
由机械能守恒得:
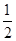 mvA2=
mvA2=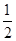 mv2+
mv2+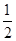 mvB2 (2分)
mvB2 (2分)联立方程解得:vA=vB=4m/s,v=0 (1分)

练习册系列答案
相关题目

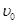 无摩擦地在车厢底板上向右运动,木块与车前壁碰撞后以
无摩擦地在车厢底板上向右运动,木块与车前壁碰撞后以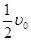 的速度向左运动,则再经过多长时间,木块将与车后壁相碰?
的速度向左运动,则再经过多长时间,木块将与车后壁相碰?
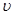 ,木箱与右侧竖直墙壁发生弹性碰撞,反弹后被小明接住,求整个过程中小明对木箱做的功.
,木箱与右侧竖直墙壁发生弹性碰撞,反弹后被小明接住,求整个过程中小明对木箱做的功.