Question

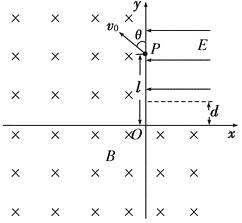
【题目】如图所示，在坐标系xOy中，第一象限除外的其它象限都充满匀强磁场，磁感应强度都为B＝0．12 T、方向垂直纸面向内。P是y轴上的一点，它到坐标原点O的距离l＝0．40 m。一比荷＝5．0×107C/kg的带正电粒子从P点开始进入匀强磁场中运动，初速度v0＝3．0×106m/s、方向与y轴正方向成夹角θ＝53°并与磁场方向垂直。不计粒子的重力作用。已知sin 53°＝0．8，cos 53°＝0．6，

求：（1）粒子在磁场中运动的轨道半径R；

（2）在第一象限中与x轴平行的虚线上方的区域内充满沿x轴负方向的匀强电场（如图），粒子在磁场中运动一段时间后进入第一象限，最后恰好从P点沿初速度的方向再次射入磁场。求匀强电场的电场强度E和电场边界（虚线）与x轴之间的距离d。

Answer 1

【答案】（1）0．50m；（2）8．0×105N/C ；0．10m

【解析】试题分析：（1）粒子在磁场区域内运动，有

可得粒子运动的轨道半径

代入数据解得：R=0．50m

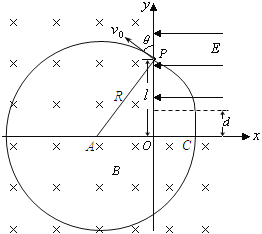
（2）通过作图可知（如图），粒子运动轨迹的圆心A恰好落在x轴上． 由几何关系可知：粒子从C点进入第一象限时的位置坐标为x=R-Rcosθ=0．20m

粒子进入匀强电场后做类平抛运动，设粒子在电场运动时间为t，加速度为a，则l-d=v0t

qE=ma

x＝at2

vx=at

粒子运动到P点时，有vx=v0tanθ

由以上各式，代入数据解得电场强度：E=8．0×105N/C

电场边界（虚线）与x轴之间的距离d=0．10m．