题目内容
13.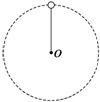 如图所示,一端固定着质量为m的小球的轻杆绕O点在竖直平面内做圆周运动,杆长为L,小球大小忽略.则下列说法中正确的是( )
如图所示,一端固定着质量为m的小球的轻杆绕O点在竖直平面内做圆周运动,杆长为L,小球大小忽略.则下列说法中正确的是( )| A. | 小球在圆周最高点时所受的向心力一定为重力 | |
| B. | 小球在最高点时杆的拉力不可能为零 | |
| C. | 若小球刚好能在竖直平面内做圆周运动,则其在最高点的速率为$\sqrt{gL}$ | |
| D. | 小球过最低点时杆对球的拉力大于重力 |
分析 杆子在最高点可以表现为拉力,也可以表现为支持力,临界的速度为零,根据牛顿第二定律进行分析.
解答 解:A、小球在最高点的最小速度为零,此时小球重所受的向心力为0.故A错误.
B、当小球在最高点拉力为零时,重力提供向心力,有mg=m$\frac{{v}^{2}}{R}$,解得v=$\sqrt{gR}$.故B错误.
C、若小球刚好能在竖直平面内做圆周运动,则其在最高点的速率为0.故C错误;
D、小球在最低点时,合力提供向心力,知合力方向向上,则拉力大于小球所受的重力.故D正确.
故选:D.
点评 解决本题的关键搞清小球向心力的来源,运用牛顿第二定律进行求解,以及知道杆子可以表现为拉力,也可以表现为支持力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.(多选)下列关于曲线运动的叙述中,正确的是( )
| A. | 做曲线运动的物体,其加速度方向一定是变化的 | |
| B. | 做曲线运动的物体,速度方向一定时刻改变 | |
| C. | 物体做曲线运动时,它所受到的合力一定不为零 | |
| D. | 物体做曲线运动时,所受合力方向有可能与速度方向在一条直线上 |
8.如图,A、B是相同的白炽灯,L是自感系数很大、电阻可忽略的自感线圈.下面说法正确的是( )


| A. | 闭合开关S时,A、B灯同时亮,且达到正常 | |
| B. | 闭合开关S时,B灯比A灯先亮,最后一样亮 | |
| C. | 闭合开关S时,A灯比B灯先亮,最后A灯比B灯更亮 | |
| D. | 断开开关S时,A灯与B灯同时慢慢熄灭 |
18.2014年3月8日马来西亚航空公司从吉隆坡飞往北京的航班MH370失联后多个国家积极投入搜救行动,在搜救过程中卫星发挥了巨大的作用.其中我国的北斗导航系统和美国的GPS导航系统均参与搜救工作.北斗导航系统包含5颗地球同步卫星,而GPS导航系统由运行周期为12小时的圆轨道卫星群组成,则下列说法正确的是( )
| A. | 发射人造地球卫星时,发射速度只要大于7.9km/s就可以 | |
| B. | 北斗同步卫星的加速度一定小于GPS卫星的加速度 | |
| C. | 北斗同步卫星的运行速度一定大于GPS卫星的运行速度 | |
| D. | 北斗同步卫星的轨道半径与GPS卫星的轨道半径之比为$\root{3}{{\frac{1}{4}}}$ |
5.在宇宙发展演化的理论中,有一种学说叫“宇宙膨胀说”,就是天体的距离在不断增大,根据这一理论,在很久很久以前,太阳系中地球的公转情况与现在相比( )
| A. | 公转半径较大 | B. | 公转周期较小 | C. | 公转周期较大 | D. | 公转角速度较大 |
3.下列实例中,物体的机械能守恒的是( )
| A. | 在空中匀速下落的跳伞运动员 | |
| B. | 沿光滑曲面自由下滑的物体 | |
| C. | 被起重机匀速吊起的重物 | |
| D. | 以$\frac{4}{5}g$的加速度竖直向上做匀减速运动的物体 |
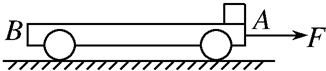
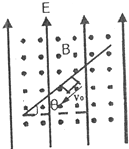 如图所示,足够长的两面均光滑的绝缘平板,固定在区域足够大的正交的方向竖直向上的匀强电场和方向水平向外的匀强磁场中,匀强电场的场强大小为E,匀强磁场的磁感强度大小为B,平板与水平面间的夹角为θ,带电荷量为+q的小物块静止在平板中央,现沿平板斜向下的方向给物块一个瞬时速度v0的同时,保持磁场(包括大小和方向)和电场的方向不变,使电场强度的大小变为3E(当地重力加速度为g),设物块沿平板运动的过程中电荷量不变),求:
如图所示,足够长的两面均光滑的绝缘平板,固定在区域足够大的正交的方向竖直向上的匀强电场和方向水平向外的匀强磁场中,匀强电场的场强大小为E,匀强磁场的磁感强度大小为B,平板与水平面间的夹角为θ,带电荷量为+q的小物块静止在平板中央,现沿平板斜向下的方向给物块一个瞬时速度v0的同时,保持磁场(包括大小和方向)和电场的方向不变,使电场强度的大小变为3E(当地重力加速度为g),设物块沿平板运动的过程中电荷量不变),求: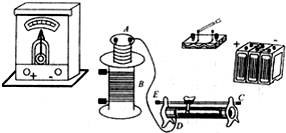 在研究电磁感应现象的实验中所用的器材如图所示.它们是:
在研究电磁感应现象的实验中所用的器材如图所示.它们是: