题目内容
18.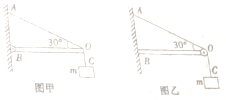 如图甲所示,轻秆OB可绕B点自由转动,另一端O点用细绳OA拉住,固定在左侧墙壁上,质量为m的重物用细绳OG悬挂在轻秆上的O点.OA与轻杆的夹角∠BOA=30°,轻杆OB水平.图乙中水平轻杆OB一端固定在竖直墙壁上,另一端O装有小滑轮,用一根细绳跨过滑轮后悬挂一质量为m的重物.图中∠BOA=30°,则:
如图甲所示,轻秆OB可绕B点自由转动,另一端O点用细绳OA拉住,固定在左侧墙壁上,质量为m的重物用细绳OG悬挂在轻秆上的O点.OA与轻杆的夹角∠BOA=30°,轻杆OB水平.图乙中水平轻杆OB一端固定在竖直墙壁上,另一端O装有小滑轮,用一根细绳跨过滑轮后悬挂一质量为m的重物.图中∠BOA=30°,则:(1)图甲、乙中细绳OA的拉力各是多大?
(2)图甲中轻杆受到的弹力是多大?
(3)图乙中轻杆对滑轮的作用力是多大?
分析 对O点受力分析,受m的拉力(等于G)、轻杆对B点的弹力和绳AO的拉力,根据共点力平衡条件并结合合成法列式求解即可.
跨过光滑定滑轮的轻绳上张力大小处处相等,滑轮对绳子的作用力应该是两滑轮两侧细绳拉力的合力,根据平衡条件和平行四边形定则求解.
解答  解(1)图甲中,以O点为研究对象,受力分析,根据平衡条件得:T=$\frac{mg}{sin30°}=2mg$,N=mgcot30°=$\sqrt{3}$mg,
解(1)图甲中,以O点为研究对象,受力分析,根据平衡条件得:T=$\frac{mg}{sin30°}=2mg$,N=mgcot30°=$\sqrt{3}$mg,
图乙中,对绳子上的O点,受力平衡,有:T=mg,
(2)由牛顿第三定律:图甲中OB杆受到的弹力N′=N=$\sqrt{3}$mg
(3)乙图中,由题意可得,对O点受力分析:
滑轮受到绳子的作用力应为图中两段绳中拉力F1和F2的合力F,
因同一根绳张力处处相等,都等于物体的重量,即F1=F2=G=mg.
用平行四边形定则作图,由于拉力F1和F2的夹角为120°,则由几何知识得:F=60N.
答:(1)图甲、乙中细绳OA的拉力分别为2mg、mg;
(2)图甲中轻杆受到的弹力是$\sqrt{3}$mg;
(3)图乙中轻杆对滑轮的作用力是mg.
点评 如果O处是结点,则OA和OC是两根绳子,其拉力不相等,若O处为滑轮,则OA和OC为一根绳子,同一根绳子上拉力相等;要注意区分.

练习册系列答案
相关题目
9.对速度和加速度的理解,以下正确的( )
| A. | 速度越大,加速度越大 | |
| B. | 速度变化越快,加速度越大,速度为零时加速度也为零 | |
| C. | 有加速度时速度一定发生变化 | |
| D. | 速度发生变化时一定有加速度 |
13.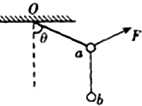 如图所示,将两个质量均为m的小球a、b用细线相连并悬挂于O点,用力F拉小球a使整个装置处于平衡状态,且悬线Oa与竖直方向的夹角为θ=60°,则力F的大小可能为 ( )
如图所示,将两个质量均为m的小球a、b用细线相连并悬挂于O点,用力F拉小球a使整个装置处于平衡状态,且悬线Oa与竖直方向的夹角为θ=60°,则力F的大小可能为 ( )
 如图所示,将两个质量均为m的小球a、b用细线相连并悬挂于O点,用力F拉小球a使整个装置处于平衡状态,且悬线Oa与竖直方向的夹角为θ=60°,则力F的大小可能为 ( )
如图所示,将两个质量均为m的小球a、b用细线相连并悬挂于O点,用力F拉小球a使整个装置处于平衡状态,且悬线Oa与竖直方向的夹角为θ=60°,则力F的大小可能为 ( )| A. | $\sqrt{3}$mg | B. | mg | C. | $\frac{\sqrt{3}}{2}$mg | D. | $\frac{\sqrt{3}}{3}$Lmg |
10.如图所示为A、B、C三个小球做平抛运动的示意图,关于三个球做平抛运动的判断正确的是( )


| A. | 三个球抛出初速度大小关系为vA>vB>vC | |
| B. | 若三个球同时抛出,则C球先落地 | |
| C. | 若三个球同时落地,则A球先抛出 | |
| D. | 若某一时刻三个球在同一竖直线上,则A球一定在最下面 |
