题目内容
1.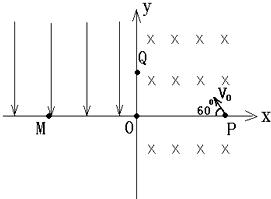 如图,在xoy平面内,y轴的右侧有垂直纸面向里的匀强磁场,y轴的左侧有沿y轴负方向的匀强电场.一质量为m、电量为q的带正电的粒子从x轴上的P点开始运动,速度大小为v0、方向与x轴负方向的夹角为60°,然后在y轴上的Q点以垂直y轴方向进入电场,最后到达y轴上的M点.已知OP=OM=d.求
如图,在xoy平面内,y轴的右侧有垂直纸面向里的匀强磁场,y轴的左侧有沿y轴负方向的匀强电场.一质量为m、电量为q的带正电的粒子从x轴上的P点开始运动,速度大小为v0、方向与x轴负方向的夹角为60°,然后在y轴上的Q点以垂直y轴方向进入电场,最后到达y轴上的M点.已知OP=OM=d.求(1)电场强度E
(2)从P到M的时间t总.
分析 (1)粒子在电场中做类平抛运动,由牛顿第二定律及运动学公式即可求出电场强度;
(2)粒子在洛仑兹力作用下做匀速圆周运动的半径根据几何关系可以求出,再由牛顿第二定律即可求出磁感应强度;分段求时间:电场中运用运动学公式求时间,磁场中粒子运动了半个周期,再求总时间.
解答  解:(1)粒子在磁场中做匀速圆周运动,根据题意画出粒子运动的轨迹如图,则:
解:(1)粒子在磁场中做匀速圆周运动,根据题意画出粒子运动的轨迹如图,则:
r=$\frac{OP}{sin60°}=\frac{2\sqrt{3}}{3}d$…①
OQ=r-OO′=r-r•cos60°=$\frac{1}{2}r=\frac{\sqrt{3}}{3}d$…②
粒子在电场中做类平抛运动,竖直方向:$OQ=\frac{1}{2}a{t}^{2}=\frac{1}{2}×\frac{qE}{m}•{t}^{2}$…③
水平方向:OM=v0t…④
代入数据得:$E=\frac{2\sqrt{3}m{v}_{0}^{2}}{3qd}$…⑤
(2)由图可知,粒子在磁场中的偏转角是60°,粒子在磁场中运动的周期:
$T=\frac{2πr}{{v}_{0}}$…⑥
所以粒子在磁场中运动的时间:$t′=\frac{60°}{360°}•T$…⑦
粒子运动的总时间:t总=t+t′…⑧
联立以上的方程得:${t}_{总}=(\frac{2\sqrt{3}π}{9}+1)\frac{d}{{v}_{0}}$
答:(1)电场强度大小是$\frac{2\sqrt{3}m{v}_{0}^{2}}{3qd}$;
(2)从P到M的时间是$(\frac{2\sqrt{3}π}{9}+1)\frac{d}{{v}_{0}}$.
点评 本题主要考查了带电粒子在混合场中运动的问题,要求同学们能正确分析粒子的受力情况,再通过受力情况分析粒子的运动情况,熟练掌握圆周运动及平抛运动的基本公式,难度适中.

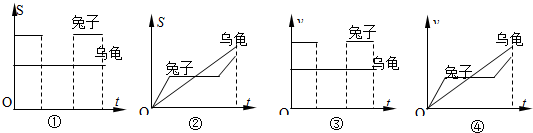
| A. | ①③ | B. | ②③ | C. | ①④ | D. | ②④ |
 如图所示,a、b两个点电荷带等量同种正电荷,位置固定,O为ab的中点,O1 O2通过O且与ab垂直,一个电子(重力可忽略)从O2一侧沿O2O1方向射入,则电子穿过O再向左运动的过程中( )
如图所示,a、b两个点电荷带等量同种正电荷,位置固定,O为ab的中点,O1 O2通过O且与ab垂直,一个电子(重力可忽略)从O2一侧沿O2O1方向射入,则电子穿过O再向左运动的过程中( )| A. | 它的电势能逐渐变大 | |
| B. | 它的电势能逐渐变小 | |
| C. | 它的加速度开始一段逐渐加大,后来逐渐减小 | |
| D. | 它的加速度开始一段逐渐减小,后来逐渐增加 |
| A. | 在电源内部把正电荷从负极移到正极,非静电力做功,电势能减少 | |
| B. | 对于给定的电源,移动正电荷非静电力做功越多,电动势越大 | |
| C. | 电动势越大,说明非静电力在电源内部从负极向正极移动单位电荷量做功越多 | |
| D. | 电动势越大,说明非静电力在电源内部把正电荷从电源负极移到正极所移动电荷量越多 |
 在一次抗洪救灾工作中,一架直升机A用长H=50m的悬索(重力可忽略不计)系住一质量m=50kg的被困人员B,直升机A和被困人员B以v0=10m/s的速度一起沿水平方向匀速运动,如图甲所示.某时刻开始收悬索将人吊起,在5s时间内,A、B之间的竖直距离以l=50-t2(单位:m)的规律变化,取g=10m/s2.求:
在一次抗洪救灾工作中,一架直升机A用长H=50m的悬索(重力可忽略不计)系住一质量m=50kg的被困人员B,直升机A和被困人员B以v0=10m/s的速度一起沿水平方向匀速运动,如图甲所示.某时刻开始收悬索将人吊起,在5s时间内,A、B之间的竖直距离以l=50-t2(单位:m)的规律变化,取g=10m/s2.求: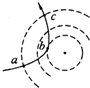 根据α粒子散射实验,卢瑟福提出了原子的核式结构模型.如图中虚线表示原子核所形成的电场的等势线,实线表示一个α粒子的运动轨迹.在α粒子从a运动到b,再运动到c的过程中,α粒子的动能先减小,后增大;电势能先增大后减小.(填“增大”“减小”或“不变”)
根据α粒子散射实验,卢瑟福提出了原子的核式结构模型.如图中虚线表示原子核所形成的电场的等势线,实线表示一个α粒子的运动轨迹.在α粒子从a运动到b,再运动到c的过程中,α粒子的动能先减小,后增大;电势能先增大后减小.(填“增大”“减小”或“不变”)
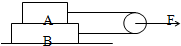 如图所示,物块B上放一容器A,质量分别是mA=2kg,mB=4kg,A、B通过绕过动滑轮的轻绳相连,滑轮的质量不变,在滑轮上加一水平拉力F.A和B、B和水平面间的动摩擦因数都等于0.3,且最大静摩擦力等于滑动摩擦力.求:
如图所示,物块B上放一容器A,质量分别是mA=2kg,mB=4kg,A、B通过绕过动滑轮的轻绳相连,滑轮的质量不变,在滑轮上加一水平拉力F.A和B、B和水平面间的动摩擦因数都等于0.3,且最大静摩擦力等于滑动摩擦力.求: