题目内容
17. 物块先沿轨道1从A点由静止下滑到底端B点,后沿轨道2从A点由静止下滑经C点至底端B点,AC=CB,如图所示,物块与两轨道的动摩擦因数相同,不考虑物块在C点处撞击的能量损失,则在物块整个下滑过程中( )
物块先沿轨道1从A点由静止下滑到底端B点,后沿轨道2从A点由静止下滑经C点至底端B点,AC=CB,如图所示,物块与两轨道的动摩擦因数相同,不考虑物块在C点处撞击的能量损失,则在物块整个下滑过程中( )| A. | 沿轨道2下滑时的时间较小 | B. | 物块下滑时损失的机械能相同 | ||
| C. | 物块在AC和CB段受到的摩擦力相同 | D. | 物块滑至B点时速度相同 |
分析 物体下滑过程中滑动摩擦力做功大小与水平位移有关,两次下滑过程,物块的位移相等,滑动摩擦力做功相等,根据动能定理分析物块滑到B点的速度大小关系,由摩擦力公式分析摩擦力的大小关系.
解答 解:摩擦力f=μmgcosθ,在轨道上倾角不同,所以物块在AC和CB段受到的摩擦力不同,
设AC与水平面的夹角为α,CB与水平面的夹角为β,AB与水平面的夹角为θ,如图所示:
沿轨道2运动,摩擦力做的功:Wf2=μmgcosα•xAC+μmgcosβ•xCB=μmg•xEF+μmg•xEB=μmg•xFB
沿轨道1运动,摩擦力做的功为:Wf1=μmgcosθ•xAB=μmg•xFB=Wf2
由动能定理$\frac{1}{2}m{v}^{2}={W}_{G}-Wf$得:物块滑至B点时速度大小相同,但方向不同,两种运动摩擦力做的功相同,所以两种情况下损失的机械能相同 ,
,
物体沿1做匀加速直线运动,沿2先做加速度比1大的加速运动,后做加速度比1小的加速运动,而运动的总位移相同,画出速度时间图象,如图所示,则沿轨道2下滑时的时间较小,故AB正确;
故CD错误
故选:AB.
点评 该题要求同学们能根据题目正确求出各个阶段摩擦力所做的功,并结合动能定理求解,解答的关键是正确判断出摩擦力做的功仅仅与水平距离的长度有关.难度适中.

练习册系列答案
相关题目
7.电场中某处的电场线如图所示,则( )


| A. | a、b两处的电场强度大小不等,Ea>Eb | |
| B. | a、b两处的电场强度大小不等,Ea<Eb | |
| C. | 同一点电荷放在a处的电场力和放在b处的电场力一样大 | |
| D. | 同一点电荷放在a处的电场力比放在b处的电场力大 |
8.关于光的波粒二象性的理解,正确的是( )
| A. | 大量的光子中有些光子表现出波动性,有些光子表现出粒子性 | |
| B. | 光在传播时是波,而与物质相互作用时就转变成粒子 | |
| C. | 高频光是粒子,低频光是波 | |
| D. | 波粒二象性是光的属性,有时它的波动性显著,有时它的粒子性显著 |
12.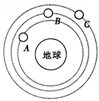 如图所示,是在同一轨道平面上运行的三颗不同的人造地球卫星,关于各相关物理量的关系,下列说法正确的是( )
如图所示,是在同一轨道平面上运行的三颗不同的人造地球卫星,关于各相关物理量的关系,下列说法正确的是( )
 如图所示,是在同一轨道平面上运行的三颗不同的人造地球卫星,关于各相关物理量的关系,下列说法正确的是( )
如图所示,是在同一轨道平面上运行的三颗不同的人造地球卫星,关于各相关物理量的关系,下列说法正确的是( )| A. | 根据v=$\sqrt{gr}$,可知线速度vA<vB<vC | |
| B. | 根据万有引力定律可知,所受的万有引力关系为FA>FB>FC | |
| C. | 角速度的关系为ωA>ωB>ωC | |
| D. | 向心加速度的关系为aA<aB<aC |
9.一定质量的理想气体密闭在容积不变的容器中,当温度降低时( )
| A. | 压强减小,密度减小 | B. | 压强增大,密度增大 | ||
| C. | 压强不变,密度减小 | D. | 压强减小,密度不变 |
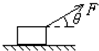 如图所示,质量m=20kg的物体放在水平地面上,现给物体施加一个与水平面成θ=37°角的斜向上的F=50N的作用力.取g=10m/s2,sin37°=0.6,cos37°=0.8,求:
如图所示,质量m=20kg的物体放在水平地面上,现给物体施加一个与水平面成θ=37°角的斜向上的F=50N的作用力.取g=10m/s2,sin37°=0.6,cos37°=0.8,求: 如图为机场行李货物传送装置简化图,由水平传送带直线AB和半圆BC两部分组成,传送带的速度大小恒为v=1m/s,AB长L=2m,圆弧半径R=1m.现将质量m=10kg的货物无初速度放上A端,货物与传送带间的动摩擦因数μ=0.5,货物能沿图中虚线轨迹运动.设最大静摩擦力等于滑动摩擦力,重力加速度g=10m/s2,求:
如图为机场行李货物传送装置简化图,由水平传送带直线AB和半圆BC两部分组成,传送带的速度大小恒为v=1m/s,AB长L=2m,圆弧半径R=1m.现将质量m=10kg的货物无初速度放上A端,货物与传送带间的动摩擦因数μ=0.5,货物能沿图中虚线轨迹运动.设最大静摩擦力等于滑动摩擦力,重力加速度g=10m/s2,求: