题目内容
20. 如图所示,半径为R的光滑圆形轨道固定在竖直面内.小球A、B质量分别为m、3m(β为待定系数).A球从左边与圆心等高处由静止开始沿轨道下滑,与静止于轨道最低点的B球相撞,碰撞中无机械能损失,重力加速度为g.试求:
如图所示,半径为R的光滑圆形轨道固定在竖直面内.小球A、B质量分别为m、3m(β为待定系数).A球从左边与圆心等高处由静止开始沿轨道下滑,与静止于轨道最低点的B球相撞,碰撞中无机械能损失,重力加速度为g.试求:(Ⅰ)第一次碰撞后A、B球能达到的最大高度各为多少?
(Ⅱ)小球A、B在轨道最低处第二次碰撞刚结束时各自的速度,并讨论小球A、B在轨道最低处第n次碰撞刚结束时各自的速度.
分析 (Ⅰ)(Ⅱ)两小球碰撞后动量守恒,机械能守恒,AB两球上升后机械能守恒,根据机械能守恒定律及动量守恒定律即可求解.
解答 解:(Ⅰ) 由机械能守恒定律知,第一次碰撞前A的速度为${v}_{1}=\sqrt{2gR}$设A、B第一次碰撞后的速度大小分别为v1′、vv2′,
mv1=mv1′+3mv2′
$mgR=\frac{1}{2}m{v′}_{1}^{2}+\frac{1}{2}•3m{v′}_{2}^{2}$
解得${v}_{1}′=\sqrt{\frac{gR}{2}}$,向左
${v}_{2}′=\sqrt{\frac{gR}{2}}$向右
由 $\frac{1}{2}mv{′}_{1}^{2}=mgh′$ 得${h}_{1}′=\frac{R}{4}$
同理,${h}_{2}′=\frac{R}{4}$
(Ⅱ)设A、B球第二次碰撞刚结束时的速度分别为V1、V2,则:
mv1′-3mv2′=mV1+3mV2
$mgR=\frac{1}{2}m{V}_{1}^{2}+\frac{1}{2}•3m{V}_{2}^{2}$
解得${V}_{1}=-\sqrt{2gR}$,V2=0
(另一组解:${V}_{1}=\sqrt{\frac{gR}{2}}$,${V}_{2}=-\sqrt{\frac{gR}{2}}$不合题意,舍去)
由此可得:当n为奇数时,小球A、B在第n次碰撞刚结束时的速度分别与其第一次碰撞刚结束时相同;当n为偶数时,小球A、B在第n次碰撞刚结束时的速度分别与其第二次碰撞刚结束时相同.
答:(Ⅰ)第一次碰撞后A、B球能达到的最大高度都是$\frac{R}{4}$;
(Ⅱ)小球A、B在轨道最低处第二次碰撞刚结束时A的速度是$-\sqrt{2gR}$,B的速度是0;当n为奇数时,小球A、B在第n次碰撞刚结束时的速度分别与其第一次碰撞刚结束时相同,分别为$\sqrt{\frac{gR}{2}}$向左,$\sqrt{\frac{gR}{2}}$向右;当n为偶数时,小球A、B在第n次碰撞刚结束时的速度分别与其第二次碰撞刚结束时相同,A的速度是$-\sqrt{2gR}$,B的速度是0.
点评 本题主要考查了机械能守恒定律及动量守恒定律的应用,把握运动的过程,分别对相应的过程列出动量守恒定律和机械能守恒的表达式即可.难度适中.

| A. | 1.5V | B. | 1.7V | C. | 1V | D. | 1.4V |
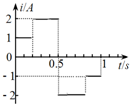
 一列简谐横波沿x轴传播,t=0时的波形如图示,质点A与质点B相距1m,A点速度沿y轴正方向;t=0.02s时,质点A第二次到达正向最大位移处,由此可知( )
一列简谐横波沿x轴传播,t=0时的波形如图示,质点A与质点B相距1m,A点速度沿y轴正方向;t=0.02s时,质点A第二次到达正向最大位移处,由此可知( )| A. | 此波沿x轴负方向传播 | |
| B. | 此波的传播速度为125m/s | |
| C. | 从t=0时起,经过0.04 s,质点A沿波传播方向迁移了5m | |
| D. | 在t=0.04 s时,质点B处在平衡位置,速度沿y轴负方向 | |
| E. | 能与该波发生干涉的横波的频率一定为62.5Hz |
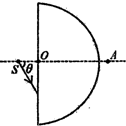 如图所示,一个半径为R、折射率为$\sqrt{3}$的透明玻璃半球体,O为球心,轴线OA水平且与半球体的左边界垂直.位于轴线上0点左侧$\frac{R}{3}$处的点光源S发出一束与OA夹角θ=60°的光线射向半球体.已知光在真空中传播的速度为c.
如图所示,一个半径为R、折射率为$\sqrt{3}$的透明玻璃半球体,O为球心,轴线OA水平且与半球体的左边界垂直.位于轴线上0点左侧$\frac{R}{3}$处的点光源S发出一束与OA夹角θ=60°的光线射向半球体.已知光在真空中传播的速度为c.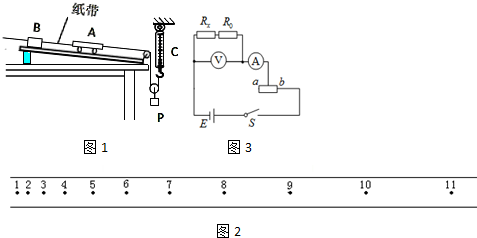



 页岩气是从页岩层中开采出来的天然气,主要成分为甲烷,被公认是洁净的能源.
页岩气是从页岩层中开采出来的天然气,主要成分为甲烷,被公认是洁净的能源.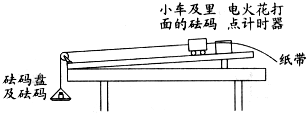 一小组的同学用如图所示的装置探究小车动能变化与合力功的关系,他们将砝码和砝码盘的重力作为小车受到的合力.
一小组的同学用如图所示的装置探究小车动能变化与合力功的关系,他们将砝码和砝码盘的重力作为小车受到的合力.