题目内容
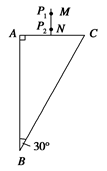
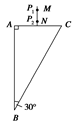
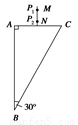
如图所示，用某种透光物质制成的三棱镜ABC，∠B=∠C=30°；在平行于BC的直线MN上插两枚大头针P1、P2，AC 边的右侧透过棱镜观察大头针P1，P2像，调整视线方向，直到Pl的像被P2的像挡住，再在AC边的右侧先后插上两枚大头针P3、P4，使P3挡住P1和P2的像，P4挡住P1、P2的像和P3，记下P3、P4的位置，移去大头针和三棱镜，发现4枚大头针的位置正好在一条直线上，该直线过AB边和AC边的中点．（1）在图中画出完整的光路图．
（2）该透光物质的折射率n为多少？
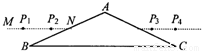
【答案】分析：（1）由题意分析可知，光线在BC面上发生了全反射，光路左右对称，作出光路图．
（2）根据几何关系确定AB面上入射角和折射角，由折射定律求折射率．
解答：
解：（1）由题：入射光线与出射光线在同一直线上，说明光线在BC面上发生了全反射，光路左右对称，作出光路图如图所示．
（2）由几何关系知：入射角θ1=60°，折射角θ2=30°
则折射率n=
=
答：
（1）画出光路图如图所示．
（2）该透光物质的折射率n为
．
点评：本题关键要抓住对称性和光路的可逆性，作出光路图，再由折射定律求折射率．
（2）根据几何关系确定AB面上入射角和折射角，由折射定律求折射率．
解答：
解：（1）由题：入射光线与出射光线在同一直线上，说明光线在BC面上发生了全反射，光路左右对称，作出光路图如图所示．（2）由几何关系知：入射角θ1=60°，折射角θ2=30°
则折射率n=
=答：
（1）画出光路图如图所示．
（2）该透光物质的折射率n为
．点评：本题关键要抓住对称性和光路的可逆性，作出光路图，再由折射定律求折射率．
练习册系列答案
相关题目
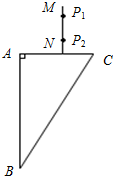如图所示，用某种透光物制成的直角三棱镜ABC；在垂直于AC面的直线MN上插两枚大头针P1、P2，在AB面的左侧透过棱镜观察大头针P1、P2的像，调整视线方向，直到P1的像
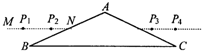如图所示，用某种透光物质制成的三棱镜ABC，∠B=∠C=30°；在平行于BC的直线MN上插两枚大头针P1、P2，AC 边的右侧透过棱镜观察大头针P1，P2像，调整视线方向，直到Pl的像被P2的像挡住，再在AC边的右侧先后插上两枚大头针P3、P4，使P3挡住P1和P2的像，P4挡住P1、P2的像和P3，记下P3、P4的位置，移去大头针和三棱镜，发现4枚大头针的位置正好在一条直线上，该直线过AB边和AC边的中点．
