题目内容
1.汽车A以vA=4m/s的速度做匀速直线运动,在A的前方相距x0=7m处,汽车B以vB=10m/s的初速度向相同方向做匀减速直线运动,加速度的大小为a=2m/s2,从此时开始计时,求:(1)A追上B前,A、B间的最大距离d是多大?
(2)经过多长时间A追上B?
分析 (1)根据速度时间公式求出两车速度相等时间内的时间,结合位移公式求出两者的位移,从而求出A、B间的最大距离.
(2)根据速度时间公式求出B速度减为零的时间,根据A、B的位移关系判断此时A是否追上B,若未追上,结合位移公式,抓住位移关系求出追及的时间.
解答 解:(1)两车速度相等经历的时间为:
${t_1}=\frac{{{v_B}-{v_A}}}{a}$=$\frac{10-4}{2}s=3s$
设A、B的最远距离为d,有:
$v_B^2-v_A^2=2a{x_{B1}}$,
${x_{A_1}}={v_A}{t_1}$,
两者间的最大距离为:
d=x0+xB1-xA1,
代入数据解得:d=16m.
(2)设B速度减为零的时间为t2,有:
0=vB-at2,得:t2=$\frac{{v}_{B}}{a}=\frac{10}{2}s$=5s
B速度减为零的位移为:${x}_{B}=\frac{{{v}_{B}}^{2}}{2a}=\frac{100}{4}m=25m$,
此时A的位移为:xA=vAt2=4×5m=20m,
因为xA<xB+x0,可知B速度减为零时,A还未追上B.
还需追及的时间:${t}_{3}=\frac{{x}_{B}+{x}_{0}-{x}_{A}}{{v}_{A}}=\frac{25+7-20}{4}s=3s$,
则有:t=t2+t3=5s+3s=8s.
答:(1)A追上B前,A、B间的最大距离d是16m;
(2)经过8s时间A追上B.
点评 本题考查了运动学中的追及问题,关键抓住位移关系,结合运动学公式进行求解,知道速度相等时,有最大距离,求解追及时间时,注意B车速度减为零后不再运动.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
11.关于匀变速直线运动的下列说法,不正确的是( )
| A. | 匀加速直线运动的速度一定与时间成正比 | |
| B. | 匀减速直线运动就是加速度为负值的运动 | |
| C. | 匀变速直线运动的速度随时间均匀变化 | |
| D. | 速度先减小再增大的运动一定不是匀变速直线运动 |
12.关于弹力,下列说法正确的是( )
| A. | 放在水平桌面上的物体对桌面的压力就是该物体的重力 | |
| B. | 压力、支持力、绳中的张力的大小都可以根据胡克定律求出 | |
| C. | 弹力的大小与物体的形变程度有关,在弹性限度内形变程度越大,弹力越大 | |
| D. | 弹力的方向总是与施力物体恢复形变的方向相同 |
9.A、B两个电阻的伏安特征曲线如图所示,下列判断正确的是( )
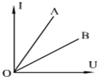

| A. | 图线表示电阻与电压成正比 | B. | 图线表示电阻与电流成反比 | ||
| C. | A的阻值小于B的阻值 | D. | A的阻值大于B的阻值 |
16.小华同学在做“研究匀变速直线运动”实验中,将打点计时器固定在某处,在绳子拉力的作用下小车拖着穿过打点计时器的纸带在水平木板上运动,如图所1示.由打点计时器得到表示小车运动过程的一条清晰纸带的一段.如图所示,在打点计时器打出的纸带上确定出八个计数点,相邻两个计数点之间的时间间隔为0.1s,并用刻度尺测出了各计数点到0计数点的距离,图2中所标数据的单位是cm.

(1)根据纸带提供的信息,小华同学已经计算出了打下1、2、3、4、5这五个计数点时小车的速度,请你帮助他计算出打下计数点6时小车的速度(结果保留3位有效数字),并填入下表.
(2)以速度v为纵轴、时间t为横轴在坐标纸上建立直角坐标系,根据表中的v、t数据,在坐标系中描点,并作出小车运动的v-t图象.(坐标系见答题卷)
(3)根据v-t图象可知,小车运动的加速度为0.43m/s2(保留2位有效数字).
(4)某同学的操作步骤如下,其中错误的步骤是AD(填代号).
A.将打点计时器固定在平板上,并接好直流电源
B.将纸带固定在小车尾部,并穿过打点计时器的限位孔
C.把一条细绳拴在小车上,细绳跨过定滑轮,下面吊着适当重的钩码
D.拉住纸带,将小车移到靠近打点计时器处先放开纸带,再接通电源
E.断开电源,取下纸带.

(1)根据纸带提供的信息,小华同学已经计算出了打下1、2、3、4、5这五个计数点时小车的速度,请你帮助他计算出打下计数点6时小车的速度(结果保留3位有效数字),并填入下表.
| 计数点 | 1 | 2 | 3 | 4 | 5 | 6 |
| t/s | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 |
| v/(m•s-1) | 0.358 | 0.400 | 0.440 | 0.485 | 0.530 | 0.570 |
(3)根据v-t图象可知,小车运动的加速度为0.43m/s2(保留2位有效数字).
(4)某同学的操作步骤如下,其中错误的步骤是AD(填代号).
A.将打点计时器固定在平板上,并接好直流电源
B.将纸带固定在小车尾部,并穿过打点计时器的限位孔
C.把一条细绳拴在小车上,细绳跨过定滑轮,下面吊着适当重的钩码
D.拉住纸带,将小车移到靠近打点计时器处先放开纸带,再接通电源
E.断开电源,取下纸带.
6.一辆公共汽车进站后开始刹车.做匀减速直线运动,开始刹车后的第1s内和第3s内位移大小依次为13m和9m,则刹车后6s内的位移是( )
| A. | 48 m | B. | 24 m | C. | 25 m | D. | 75 m |
13.如图所示,杂技演员站在一块被他踩成斜面的木板上处于静止状态,关于斜面对演员的作用力,下面说法正确的是( )

| A. | 木板对人可能有摩擦力作用,也可能没有摩擦力作用 | |
| B. | 木板对人一定有摩擦 | |
| C. | 木板对人的弹力方向一定竖直向上 | |
| D. | 木板对人的作用力方向垂直板斜向上 |
 如图所示,平行金属带电极板A、B间可看作匀强电场,场强E=1.2×103V/m,极板间距离d=5cm,电场中C和D分别到A、B两板的距离均为1cm,B极板接地,求:
如图所示,平行金属带电极板A、B间可看作匀强电场,场强E=1.2×103V/m,极板间距离d=5cm,电场中C和D分别到A、B两板的距离均为1cm,B极板接地,求: