题目内容
11.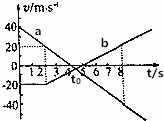 如图所示,a、b分别是甲、乙两辆车沿同一直线同时运动的图线,零时刻甲乙两车相距95m,由图线求:
如图所示,a、b分别是甲、乙两辆车沿同一直线同时运动的图线,零时刻甲乙两车相距95m,由图线求:(1)在相遇前两辆车相距的最大距离;
(2)两车何时相遇.
分析 在v-t图象中,图线的斜率大小等于加速度,根据斜率的大小分析加速度大小的关系.速度图线与坐标轴所围“面积”等于位移,并结合两车的运动情况,确定最远的距离,根据相遇时位移之差为95m列式求解时间即可.
解答 解:(1)当甲乙两车速度相等时相距最远,根据a、b两条直线的解析式:a直线:v=-10t+40 (m/s),b直线:v=$\frac{20}{3}$t-$\frac{100}{3}$(m/s),运用数学知识算出交点的横坐标为 t=$\frac{22}{5}$s,纵坐标为 v=-4m/s,由图象法可知此时a、b的距离为 S=($\frac{40×4}{2}-\frac{1}{2}×$0.4×4)+(20×2+$\frac{20+4}{2}$)+95=243m.
(2)设速度相等后,经过时间t,两车相遇,则两个速度图象与坐标轴围成的面积之和为S,
此时a的速度大小${v}_{1}=10(t+\frac{22}{5})-40=10t+4(m/s)$,b的速度大小为v2=$\frac{20}{3}t-4$(m/s),
则有:S=$\frac{1}{2}t•({v}_{1}+{v}_{2})$
解得:t=5.4s
则相遇的时间为$t′=\frac{22}{5}+5.4=9.8s$
答:(1)在相遇前两辆车相距的最大距离为243m;
(2)两车在9.8s末相遇.
点评 本题考查对速度-时间图象的理解与应用的能力.要明确斜率表示加速度,图象与坐标轴围成的面积表示位移.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
1.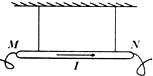 如图所示,用两根相同的细绝缘绳水平悬挂一段均匀载流导体棒MN,导体棒垂直置于匀强磁场(未画出)中,电流I方向从M到N,导体棒的质量为m,每段绳子的拉力均为F.重力加速度为g,若I大小不变,下列说法正确的是( )
如图所示,用两根相同的细绝缘绳水平悬挂一段均匀载流导体棒MN,导体棒垂直置于匀强磁场(未画出)中,电流I方向从M到N,导体棒的质量为m,每段绳子的拉力均为F.重力加速度为g,若I大小不变,下列说法正确的是( )
 如图所示,用两根相同的细绝缘绳水平悬挂一段均匀载流导体棒MN,导体棒垂直置于匀强磁场(未画出)中,电流I方向从M到N,导体棒的质量为m,每段绳子的拉力均为F.重力加速度为g,若I大小不变,下列说法正确的是( )
如图所示,用两根相同的细绝缘绳水平悬挂一段均匀载流导体棒MN,导体棒垂直置于匀强磁场(未画出)中,电流I方向从M到N,导体棒的质量为m,每段绳子的拉力均为F.重力加速度为g,若I大小不变,下列说法正确的是( )| A. | 若F<$\frac{mg}{2}$,则磁场垂直纸面向外,可增大磁感应强度使绳子拉力为零 | |
| B. | 若F<$\frac{mg}{2}$,则磁场垂直纸面向里,可增大磁感应强度使绳子拉力为零 | |
| C. | 若F>$\frac{mg}{2}$,则磁场垂直纸面向外,可减小磁感应强度使绳子拉力为零 | |
| D. | 若F>$\frac{mg}{2}$,则磁场垂直纸面向外,改变电流方向可能使绳子拉力为零 |
2.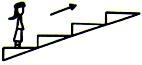 为了节省能量,某商场安装了智能化的电动扶梯.无人乘行时,扶梯运转得很慢;有人站上梯时,它会先慢慢加速,再匀速运转,一顾客乘扶梯上搂,恰好经历了这两个过程,如图所示.则在加速过程中,下列说法中正确的是( )
为了节省能量,某商场安装了智能化的电动扶梯.无人乘行时,扶梯运转得很慢;有人站上梯时,它会先慢慢加速,再匀速运转,一顾客乘扶梯上搂,恰好经历了这两个过程,如图所示.则在加速过程中,下列说法中正确的是( )
 为了节省能量,某商场安装了智能化的电动扶梯.无人乘行时,扶梯运转得很慢;有人站上梯时,它会先慢慢加速,再匀速运转,一顾客乘扶梯上搂,恰好经历了这两个过程,如图所示.则在加速过程中,下列说法中正确的是( )
为了节省能量,某商场安装了智能化的电动扶梯.无人乘行时,扶梯运转得很慢;有人站上梯时,它会先慢慢加速,再匀速运转,一顾客乘扶梯上搂,恰好经历了这两个过程,如图所示.则在加速过程中,下列说法中正确的是( )| A. | 顾客受到三个力的作用 | B. | 顾客处于失重状态 | ||
| C. | 扶梯对顾客没有摩擦力的作用 | D. | 顾客对扶梯的压力等于顾客的重量 |
16.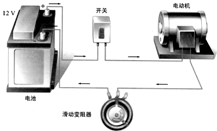 如图所示的电路,电源电动势为12V,内阻恒定且不可忽略.初始时刻,电路中的电流等于I0,且观察到电动机正常转动.现在调节滑动变阻器使电路中的电流减小为I0的一半,观察到电动机仍在转动.不考虑温度对电阻的影响,下列说法正确的是( )
如图所示的电路,电源电动势为12V,内阻恒定且不可忽略.初始时刻,电路中的电流等于I0,且观察到电动机正常转动.现在调节滑动变阻器使电路中的电流减小为I0的一半,观察到电动机仍在转动.不考虑温度对电阻的影响,下列说法正确的是( )
 如图所示的电路,电源电动势为12V,内阻恒定且不可忽略.初始时刻,电路中的电流等于I0,且观察到电动机正常转动.现在调节滑动变阻器使电路中的电流减小为I0的一半,观察到电动机仍在转动.不考虑温度对电阻的影响,下列说法正确的是( )
如图所示的电路,电源电动势为12V,内阻恒定且不可忽略.初始时刻,电路中的电流等于I0,且观察到电动机正常转动.现在调节滑动变阻器使电路中的电流减小为I0的一半,观察到电动机仍在转动.不考虑温度对电阻的影响,下列说法正确的是( )| A. | 电源的热功率减为初始时的一半 | |
| B. | 电源的总功率减为初始时的一半 | |
| C. | 电动机的热功率减为初始时的一半 | |
| D. | 变阻器的功率减为初始时的四分之一 |
20.下列关于时间和时刻的说法不正确的是( )
| A. | 8点45分开始上课,指的是时间 | |
| B. | 4秒初与5秒末的时间间隔为2秒 | |
| C. | 2秒内指的是时间 | |
| D. | 列车在9点25分到达南京站,指的是时刻 |
1.下列关于坐标系的说法错误的是( )
| A. | 为了定量描述物体的位置随时间的变化规律,我们可以在参考系上建立适当的坐标系 | |
| B. | 坐标系应该包含原点、正方向和单位长度 | |
| C. | 坐标系是在参考系的基础上抽象出来的概念,是抽象化的参考系,是为定量描述物体的位置和位置变化而引入的 | |
| D. | 对于质点的直线运动,为了研究问题的方便,一般应建立二维坐标系 |

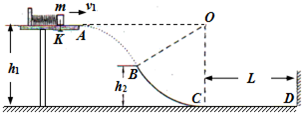 如图所示,在距水平地面高h1=1.2m的光滑水平台面上,一个质量m=1kg的小物块压缩弹簧后被锁扣K锁住,储存了一定量的弹性势能Ep.现打开锁扣K,物块与弹簧分离后将以一定的水平速度v1向右滑离平台,并恰好从B点沿切线方向进入光滑竖直的圆弧轨道BC.已知B点距水平地面的高h 2=0.6m,圆弧轨道BC的圆心O与水平台面等高,C点的切线水平,并与水平地面上长为L=2.8m的粗糙直轨道CD平滑连接,小物块与右边的竖直墙壁发生碰撞可以等速率反弹,重力加速度g=10m/s2,空气阻力忽略不计.试求:
如图所示,在距水平地面高h1=1.2m的光滑水平台面上,一个质量m=1kg的小物块压缩弹簧后被锁扣K锁住,储存了一定量的弹性势能Ep.现打开锁扣K,物块与弹簧分离后将以一定的水平速度v1向右滑离平台,并恰好从B点沿切线方向进入光滑竖直的圆弧轨道BC.已知B点距水平地面的高h 2=0.6m,圆弧轨道BC的圆心O与水平台面等高,C点的切线水平,并与水平地面上长为L=2.8m的粗糙直轨道CD平滑连接,小物块与右边的竖直墙壁发生碰撞可以等速率反弹,重力加速度g=10m/s2,空气阻力忽略不计.试求: