题目内容
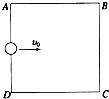 如图所示,竖直面内的正方形ABCD的边长为d,质量为m、电荷量为+q的小球从AD边的中点,以某一初速度进入正方形区域.若正方形区域内未加电场时,小球恰好从CD边的中点离开正方形区域;若在正方形区域内加上竖直方向的匀强电场,小球可以从BC边离开正方形区域.已知重力加速度为g,求:
如图所示,竖直面内的正方形ABCD的边长为d,质量为m、电荷量为+q的小球从AD边的中点,以某一初速度进入正方形区域.若正方形区域内未加电场时,小球恰好从CD边的中点离开正方形区域;若在正方形区域内加上竖直方向的匀强电场,小球可以从BC边离开正方形区域.已知重力加速度为g,求:(1)小球进入正方形区域的初速度V0.
(2)要使小球从BC边离开正方形区域,求所加竖直方向的匀强电场的场强E的方向和E的大小范围.
分析:(1)未加电场时小球在重力作用下做平抛运动,由平抛运动的规律可求得小球进入正方形区域的初速度;
(2)要使小球从BC边离开正方形区域则临界值为刚好从B、C点离开,则由类平抛运动的规律可得出粒子从BC边离开的场强的方向和大小.
(2)要使小球从BC边离开正方形区域则临界值为刚好从B、C点离开,则由类平抛运动的规律可得出粒子从BC边离开的场强的方向和大小.
解答:解:(1)未知电场时,小球做平抛运动,由平抛运动公式:
水平方向:
=v0t
竖直方向:
=
gt2
解得:v0=
(2)要使小球从BC边离开正方形区域,应加竖直向上的匀强电场.
小球从C点离开正方形时,设场强为E1,由牛顿第二定律:mg-qE1=ma1
初速度方向位移:d=v0t1
垂直初速度方向位移:
=
a1
解得:E1=
小球从B点离开正方形时,设场强为E2,由牛顿第二定律:qE2-mg=ma2
初速度方向位移:d=v0t2
垂直初速度方向位移:
=
a2
解得:E2=
场强E的大小范围为:
≤E≤
;
答:(1)粒子的速度为
;
(2)场强的范围为
≤E≤
,电场方向竖直向上.
水平方向:
| d |
| 2 |
竖直方向:
| d |
| 2 |
| 1 |
| 2 |
解得:v0=
| ||
| 2 |
(2)要使小球从BC边离开正方形区域,应加竖直向上的匀强电场.
小球从C点离开正方形时,设场强为E1,由牛顿第二定律:mg-qE1=ma1
初速度方向位移:d=v0t1
垂直初速度方向位移:
| d |
| 2 |
| 1 |
| 2 |
| t | 2 1 |
解得:E1=
| 3mg |
| 4q |
小球从B点离开正方形时,设场强为E2,由牛顿第二定律:qE2-mg=ma2
初速度方向位移:d=v0t2
垂直初速度方向位移:
| d |
| 2 |
| 1 |
| 2 |
| t | 2 2 |
解得:E2=
| 5mg |
| 4q |
场强E的大小范围为:
| 3mg |
| 4q |
| 5mg |
| 4q |
答:(1)粒子的速度为
| ||
| 2 |
(2)场强的范围为
| 3mg |
| 4q |
| 5mg |
| 4q |
点评:解决本题的关键在于正确分析小球的运动情况,找出粒子满足条件的临界条件:即从B和从C点离开时小球的水平位移和竖直位移,再从牛顿第二定律及运动的合成与分解规律求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
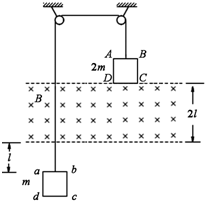 如图所示,竖直面内的正方形导线框ABCD、abcd的边长均为l、电阻均为R,质量分别为2m和m,它们分别系在一跨过两个定滑轮的轻绳两端,在两导线框之间有一宽度为2l、磁感应强度大小为B、方向垂直竖直面向里的匀强磁场.开始时ABCD的下边与匀强磁场的上边界重合,abcd的上边到匀强磁场的下边界的距离为l.现将系统由静止释放,当ABCD刚全部进入磁场时,系统开始做匀速运动.不计摩擦和空气阻力,求:
如图所示,竖直面内的正方形导线框ABCD、abcd的边长均为l、电阻均为R,质量分别为2m和m,它们分别系在一跨过两个定滑轮的轻绳两端,在两导线框之间有一宽度为2l、磁感应强度大小为B、方向垂直竖直面向里的匀强磁场.开始时ABCD的下边与匀强磁场的上边界重合,abcd的上边到匀强磁场的下边界的距离为l.现将系统由静止释放,当ABCD刚全部进入磁场时,系统开始做匀速运动.不计摩擦和空气阻力,求: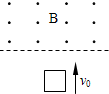 (2008?惠州三模)如图所示,竖直面内的虚线上方是一匀强磁场B,从虚线下方竖直上抛一正方形线圈,线圈越过虚线进入磁场,最后又落回到原处,运动过程中线圈平面保持在竖直面内,不计空气阻力,则( )
(2008?惠州三模)如图所示,竖直面内的虚线上方是一匀强磁场B,从虚线下方竖直上抛一正方形线圈,线圈越过虚线进入磁场,最后又落回到原处,运动过程中线圈平面保持在竖直面内,不计空气阻力,则( )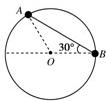 (2010?桂林二模)如图所示,竖直面内的固定圆环光滑,两个有孔的小球A和B套在环上.中间用一根轻绳相连,B处在过圆心的水平线上,绳与水平方向的夹角为30°时A、B均保持静止,已知B的质量为m,下列判断正确的是( )
(2010?桂林二模)如图所示,竖直面内的固定圆环光滑,两个有孔的小球A和B套在环上.中间用一根轻绳相连,B处在过圆心的水平线上,绳与水平方向的夹角为30°时A、B均保持静止,已知B的质量为m,下列判断正确的是( )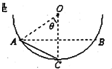 如图所示为竖直面内的光滑半圆弧轨道,O为圆心,A、B是位于同一水平线的圆弧上的两点,C为圆弧最低点,AC间有一光滑直杆,OA与竖直方向的夹角为θ.现有可视为质点的两个甲乙小球分别套在AC直杆、BC圆弧上(图中未画出),另一可视为质点的小球丙处于D点.现让甲、乙、丙三小球分别从A、B、O点无初速释放,到达C处所经过的时间分别为t1、t2、t3,不计空气阻力,不考虑三小球的碰撞,则关于时间t1、t2、t3的大小关系,下列说法正确的是( )
如图所示为竖直面内的光滑半圆弧轨道,O为圆心,A、B是位于同一水平线的圆弧上的两点,C为圆弧最低点,AC间有一光滑直杆,OA与竖直方向的夹角为θ.现有可视为质点的两个甲乙小球分别套在AC直杆、BC圆弧上(图中未画出),另一可视为质点的小球丙处于D点.现让甲、乙、丙三小球分别从A、B、O点无初速释放,到达C处所经过的时间分别为t1、t2、t3,不计空气阻力,不考虑三小球的碰撞,则关于时间t1、t2、t3的大小关系,下列说法正确的是( )