题目内容
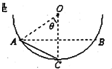 如图所示为竖直面内的光滑半圆弧轨道,O为圆心,A、B是位于同一水平线的圆弧上的两点,C为圆弧最低点,AC间有一光滑直杆,OA与竖直方向的夹角为θ.现有可视为质点的两个甲乙小球分别套在AC直杆、BC圆弧上(图中未画出),另一可视为质点的小球丙处于D点.现让甲、乙、丙三小球分别从A、B、O点无初速释放,到达C处所经过的时间分别为t1、t2、t3,不计空气阻力,不考虑三小球的碰撞,则关于时间t1、t2、t3的大小关系,下列说法正确的是( )
如图所示为竖直面内的光滑半圆弧轨道,O为圆心,A、B是位于同一水平线的圆弧上的两点,C为圆弧最低点,AC间有一光滑直杆,OA与竖直方向的夹角为θ.现有可视为质点的两个甲乙小球分别套在AC直杆、BC圆弧上(图中未画出),另一可视为质点的小球丙处于D点.现让甲、乙、丙三小球分别从A、B、O点无初速释放,到达C处所经过的时间分别为t1、t2、t3,不计空气阻力,不考虑三小球的碰撞,则关于时间t1、t2、t3的大小关系,下列说法正确的是( )分析:物体沿着位于同一竖直圆上所有光滑细杆由静止下滑,到达圆周最低点的时间相等,所有无论θ多大,t1是不变的,从B点释放做圆周运动,从O点释放做自由落体运动,根据运动学基本公式表示出运动的时间即可比较.
解答:解:物体沿着位于同一竖直圆上所有光滑细杆由静止下滑,到达圆周最低点的时间相等,所有无论θ多大,t1是不变的,
证明如下:
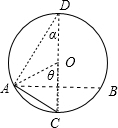
由几何关系可知lAC=2Rsinα
物体从A运动到C的过程中加速度a=gsinα
根据匀加速运动位移时间公式得:2Rsinα=
gsinαt2
解得:t=
所有无论θ多大,物体从A运动到C的时间都为t1=
,
从O点释放做自由落体运动,t3=
所以t1>t3,故A错误
从B点释放,若角度较小,则从B点释放做单摆运动,
所以t2=
=
×2π
=
,所以t1>t2,
当θ=90°时,t1<t2,故BC错误,D正确.
故选D
证明如下:

由几何关系可知lAC=2Rsinα
物体从A运动到C的过程中加速度a=gsinα
根据匀加速运动位移时间公式得:2Rsinα=
| 1 |
| 2 |
解得:t=
|
所有无论θ多大,物体从A运动到C的时间都为t1=
|
从O点释放做自由落体运动,t3=
|
所以t1>t3,故A错误
从B点释放,若角度较小,则从B点释放做单摆运动,
所以t2=
| T |
| 4 |
| 1 |
| 4 |
|
| π |
| 2 |
|
当θ=90°时,t1<t2,故BC错误,D正确.
故选D
点评:本题要求同学们知道等时圆的概念,即物体沿着位于同一竖直圆上所有光滑细杆由静止下滑,到达圆周最低点的时间相等,难度适中.

练习册系列答案
相关题目
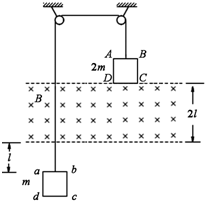 如图所示,竖直面内的正方形导线框ABCD、abcd的边长均为l、电阻均为R,质量分别为2m和m,它们分别系在一跨过两个定滑轮的轻绳两端,在两导线框之间有一宽度为2l、磁感应强度大小为B、方向垂直竖直面向里的匀强磁场.开始时ABCD的下边与匀强磁场的上边界重合,abcd的上边到匀强磁场的下边界的距离为l.现将系统由静止释放,当ABCD刚全部进入磁场时,系统开始做匀速运动.不计摩擦和空气阻力,求:
如图所示,竖直面内的正方形导线框ABCD、abcd的边长均为l、电阻均为R,质量分别为2m和m,它们分别系在一跨过两个定滑轮的轻绳两端,在两导线框之间有一宽度为2l、磁感应强度大小为B、方向垂直竖直面向里的匀强磁场.开始时ABCD的下边与匀强磁场的上边界重合,abcd的上边到匀强磁场的下边界的距离为l.现将系统由静止释放,当ABCD刚全部进入磁场时,系统开始做匀速运动.不计摩擦和空气阻力,求: 如图所示为竖直面内的光滑半圆弧轨道,O为圆心,A、B是位于同一水平线的圆弧上的两点,C为圆弧最低点,AC间有一光滑直杆,OA与竖直方向的夹角为θ.现有可视为质点的两个甲乙小球分别套在AC直杆、BC圆弧上(图中未画出),另一可视为质点的小球丙处于D点.现让甲、乙、丙三小球分别从A、B、O点无初速释放,到达C处所经过的时间分别为t1、t2、t3,不计空气阻力,不考虑三小球的碰撞,则关于时间t1、t2、t3的大小关系,下列说法正确的是
如图所示为竖直面内的光滑半圆弧轨道,O为圆心,A、B是位于同一水平线的圆弧上的两点,C为圆弧最低点,AC间有一光滑直杆,OA与竖直方向的夹角为θ.现有可视为质点的两个甲乙小球分别套在AC直杆、BC圆弧上(图中未画出),另一可视为质点的小球丙处于D点.现让甲、乙、丙三小球分别从A、B、O点无初速释放,到达C处所经过的时间分别为t1、t2、t3,不计空气阻力,不考虑三小球的碰撞,则关于时间t1、t2、t3的大小关系,下列说法正确的是
