题目内容
12. 加速电场和偏转磁场是质谱仪的两大重要组成部分.如图为质谱仪的原理简图,设想有一个静止的质量为m、带电量为q的粒子(不计重力),经电压为U的加速电场加速后垂直进入磁感应强度为B的偏转磁场中,带电粒子打至底片上的P点,设OP=x,则在图中能正确反映x与U之间函数关系的是( )
加速电场和偏转磁场是质谱仪的两大重要组成部分.如图为质谱仪的原理简图,设想有一个静止的质量为m、带电量为q的粒子(不计重力),经电压为U的加速电场加速后垂直进入磁感应强度为B的偏转磁场中,带电粒子打至底片上的P点,设OP=x,则在图中能正确反映x与U之间函数关系的是( )| A. |  | B. |  | C. |  | D. | 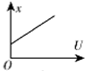 |
分析 根据动能定理$qU=\frac{1}{2}m{v}^{2}$以及粒子在磁场中偏转洛伦兹力提供向心力$qvB=\frac{m{v}^{2}}{R}$得出x与U的关系
解答 解:根据动能定理$qU=\frac{1}{2}m{v}^{2}$得,v=$\sqrt{\frac{2qU}{m}}$.粒子在磁场中偏转洛伦兹力提供向心力$qvB=\frac{m{v}^{2}}{R}$,则R=$\frac{mv}{qB}$.x=2R=$\frac{2}{B}\sqrt{\frac{2qU}{m}}$.知x∝$\sqrt{U}$.故B正确,A、C、D错误.
故选:B
点评 解决本题的关键根据动能定理$qU=\frac{1}{2}m{v}^{2}$得出速度,再利用洛伦兹力提供向心力$qvB=\frac{m{v}^{2}}{R}$得出轨道半径

练习册系列答案
相关题目
2. 如图所示,一个小孩在公园里滑滑梯.他在同一高度处分别沿两个滑梯从静止滑到水平地面上,假设小孩沿两个滑梯滑下过程中受到的摩擦力大小相等,在不考虑空气阻力的情况下,下列说法正确的是( )
如图所示,一个小孩在公园里滑滑梯.他在同一高度处分别沿两个滑梯从静止滑到水平地面上,假设小孩沿两个滑梯滑下过程中受到的摩擦力大小相等,在不考虑空气阻力的情况下,下列说法正确的是( )
 如图所示,一个小孩在公园里滑滑梯.他在同一高度处分别沿两个滑梯从静止滑到水平地面上,假设小孩沿两个滑梯滑下过程中受到的摩擦力大小相等,在不考虑空气阻力的情况下,下列说法正确的是( )
如图所示,一个小孩在公园里滑滑梯.他在同一高度处分别沿两个滑梯从静止滑到水平地面上,假设小孩沿两个滑梯滑下过程中受到的摩擦力大小相等,在不考虑空气阻力的情况下,下列说法正确的是( )| A. | 小孩两次滑下过程中重力做功不相等 | |
| B. | 小孩两次滑下过程中重力势能的减少量不相等 | |
| C. | 小孩沿直滑梯滑下到达底端时的动能小 | |
| D. | 小孩沿直滑梯滑下时,机械能损失少 |
20. 如图所示,一个质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度为$\frac{3g}{4}$,这物体在斜面上上升的最大高度为h,则在这个过程中物体( )
如图所示,一个质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度为$\frac{3g}{4}$,这物体在斜面上上升的最大高度为h,则在这个过程中物体( )
 如图所示,一个质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度为$\frac{3g}{4}$,这物体在斜面上上升的最大高度为h,则在这个过程中物体( )
如图所示,一个质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面,其运动的加速度为$\frac{3g}{4}$,这物体在斜面上上升的最大高度为h,则在这个过程中物体( )| A. | 重力势能增加了mgh | B. | 重力势能增加了$\frac{3mgh}{4}$ | ||
| C. | 动能损失了mgh | D. | 机械能损失了$\frac{mgh}{2}$ |
7. 如图所示电路,开始时K处于断开状态,A1、A2、V1、V2示数分别为I1、I2、U1、U2,现将K闭合,下列对各表读数的变化情况判断正确的是( )
如图所示电路,开始时K处于断开状态,A1、A2、V1、V2示数分别为I1、I2、U1、U2,现将K闭合,下列对各表读数的变化情况判断正确的是( )
 如图所示电路,开始时K处于断开状态,A1、A2、V1、V2示数分别为I1、I2、U1、U2,现将K闭合,下列对各表读数的变化情况判断正确的是( )
如图所示电路,开始时K处于断开状态,A1、A2、V1、V2示数分别为I1、I2、U1、U2,现将K闭合,下列对各表读数的变化情况判断正确的是( )| A. | U1减小 | B. | U2增大 | C. | I1增大 | D. | I2增大 |
17.原来静止的列车在水平轨道上以恒定的功率启动,在启动后的一小段时间内(列车所受阻力恒定)( )
| A. | 列车做匀加速直线运动 | B. | 列车做加速度逐渐减小的加速运动 | ||
| C. | 列车的速度先增大后减小 | D. | 列车的加速度先增大后减小 |
4. 如图所示,长为L的轻绳,一端拴一个质量为m的小球,另一端可绕光滑的水平轴转动,使小球始终在竖直平面内做完整的圆周运动,则(不计空气阻力,重力加速度为g)( )
如图所示,长为L的轻绳,一端拴一个质量为m的小球,另一端可绕光滑的水平轴转动,使小球始终在竖直平面内做完整的圆周运动,则(不计空气阻力,重力加速度为g)( )
 如图所示,长为L的轻绳,一端拴一个质量为m的小球,另一端可绕光滑的水平轴转动,使小球始终在竖直平面内做完整的圆周运动,则(不计空气阻力,重力加速度为g)( )
如图所示,长为L的轻绳,一端拴一个质量为m的小球,另一端可绕光滑的水平轴转动,使小球始终在竖直平面内做完整的圆周运动,则(不计空气阻力,重力加速度为g)( )| A. | 小球运动过程中速度的最小值为 $\sqrt{gL}$ | |
| B. | 小球运动到最低点时速度的最小值为 $\sqrt{5gL}$ | |
| C. | 小球运动过程中,最低点和最高点轻绳拉力的差恒为6mg | |
| D. | 小球运动过程中,最低点和最高点轻绳拉力的差不恒定,和速度大小有关 |
2.下列单位不属于国际单位制基本单位的是( )
| A. | 千克 | B. | 米 | C. | 牛顿 | D. | 秒 |

