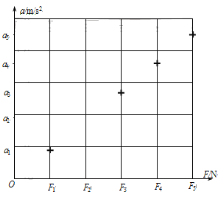
题目内容
【题目】如图所示,倾角为θ=37°的斜面放在水平地面上,小球从斜面顶端P点以初速度v0水平抛出,刚好落在斜面中点处。现将小球以初速度2v0水平抛出,不计空气阻力,小球下落后均不弹起,sin37°=0.6,cos37°=0.8,重力加速度为g,则小球两次在空中运动过程中( )
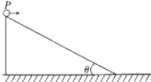
A.时间之比为1:2B.时间之比为1:![]()
C.水平位移之比为1:4D.竖直位移之比为1:2
【答案】BD
【解析】
第一次落到斜面中点,假设第二定落到水平面上,根据
![]()
可知
![]()
水平方向做匀速直线运动,根据
![]()
代入数据可知
![]()
![]()
由于第一次恰好落到斜面中点处,因此第二定一定落到水平面上,假设成立。
因此运动时间之比![]() ;水平位移之比为
;水平位移之比为![]() ;竖直位移之比为1:2。
;竖直位移之比为1:2。
BD正确,AC错误。
故选BD。

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目