题目内容
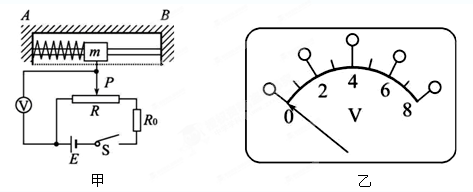
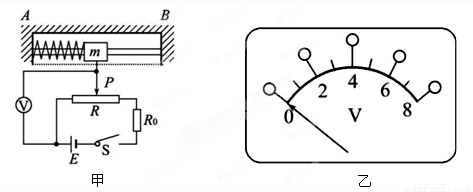
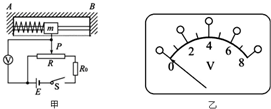 如图甲所示为加速度计的原理图:支架AB固定在待测系统上,滑块穿在AB之间的水平光滑杆上,并用轻弹簧连接在A端,其下端有一活动臂可在滑动变阻器上自由滑动.随着系统沿水平方向做变速运动,滑块相对于支架将发生位移,并通过电路转换成电信号从电压表输出.已知电压表量程为8V,滑块质量m=0.1kg,弹簧劲度系数k=20N/m,电源电动势E=10V,内阻不计,滑动变阻器总电阻值R=40Ω,有效总长度l=8cm.当待测系统静止时,滑动触头P位于变阻器R的中点,取A→B方向为正方向.
如图甲所示为加速度计的原理图:支架AB固定在待测系统上,滑块穿在AB之间的水平光滑杆上,并用轻弹簧连接在A端,其下端有一活动臂可在滑动变阻器上自由滑动.随着系统沿水平方向做变速运动,滑块相对于支架将发生位移,并通过电路转换成电信号从电压表输出.已知电压表量程为8V,滑块质量m=0.1kg,弹簧劲度系数k=20N/m,电源电动势E=10V,内阻不计,滑动变阻器总电阻值R=40Ω,有效总长度l=8cm.当待测系统静止时,滑动触头P位于变阻器R的中点,取A→B方向为正方向.(1)该加速度计能测量的最大加速度为
(2)为保证电压表能正常使用,图甲电路中电阻R0至少
(3)根据R0的最小值,将电压表盘上的电压刻度改成适当的加速度刻度,如图乙,电压4V对应加速度为
分析:(1)P端左右移动最多4cm,弹簧最大形变量0.04m,根据胡克定律和牛顿第二定律求得加速度的测量范围,即知道测量加速度的最大值.
(2)当P在最右端时,电压表读数最大,当读数为8V时,根据闭合电路欧姆定律求R0的最小值.
(3)电压表测量滑动变阻器左侧部分的电压,由闭合电路欧姆定律可得出电压的表达式;由弹簧的移动可得出此时的受到的弹力,由牛顿第二定律可得出加速度与电压间的关系;根据加速度与电压的关系式,求出不同电压值时的加速度值.
(2)当P在最右端时,电压表读数最大,当读数为8V时,根据闭合电路欧姆定律求R0的最小值.
(3)电压表测量滑动变阻器左侧部分的电压,由闭合电路欧姆定律可得出电压的表达式;由弹簧的移动可得出此时的受到的弹力,由牛顿第二定律可得出加速度与电压间的关系;根据加速度与电压的关系式,求出不同电压值时的加速度值.
解答:解:(1)P端左右移动最多4cm,弹簧最大形变量0.04m,物体加速度大小为a=
=
m/s2=8m/s2.
所以该加速度的最大值为8m/s2.
(2)当P在最右端时,电压表读数最大,当读数为8V时,Ro两端电压为U0=E-UV=10V-8V=2V
由
=
,得R0=
R=
×40Ω=10Ω
(3)当加速度向左,大小为a时,弹簧的形变量为x,电压表的输出电压为UV.则
kx=ma
又 UV=
E=
E
代入解得,UV=4+0.5a.
同理,当加速度向右大小为a时,弹簧的形变量△x电压表的输出电压,UV=4-0.5a.
以加速度向右为正.由电压和加速度的关系U=4-0.5a
当U=4V时,a =0m/s2;当U=6V,a=-4m/s2;
故答案为:(1)8m/s2.(2)10Ω.(3)0;-4
| kx |
| m |
| 20×0.04 |
| 0.1 |
所以该加速度的最大值为8m/s2.
(2)当P在最右端时,电压表读数最大,当读数为8V时,Ro两端电压为U0=E-UV=10V-8V=2V
由
| R |
| R0 |
| Uv |
| U0 |
| U0 |
| Uv |
| 2 |
| 8 |
(3)当加速度向左,大小为a时,弹簧的形变量为x,电压表的输出电压为UV.则
kx=ma
又 UV=
| R′ |
| R+R0 |
| ||||
| R+R0 |
代入解得,UV=4+0.5a.
同理,当加速度向右大小为a时,弹簧的形变量△x电压表的输出电压,UV=4-0.5a.
以加速度向右为正.由电压和加速度的关系U=4-0.5a
当U=4V时,a =0m/s2;当U=6V,a=-4m/s2;
故答案为:(1)8m/s2.(2)10Ω.(3)0;-4
点评:本题将力学与电学有机的结合在一起,考查了学生分析能力及综合考虑问题的能力,是一道不可多得的好题;解题的关键是通过弹簧的变化量把电路与牛顿第二定律连接起来.

练习册系列答案
相关题目