题目内容
7.两根完全相同的金属导线a和b,如果把其中的一个a均匀拉长到原来的两倍,把另一根导线对折后绞合起来,则它们的电阻之比为多少?分析 电阻定律:导体的电阻R跟它的长度L成正比,跟它的横截面积S成反比,还跟导体的材料有关系,这个规律就叫电阻定律,公式为R=ρ $\frac{L}{S}$.其中ρ为制成电阻的材料电阻率,L为绕制成电阻的导线长度,S为绕制成电阻的导线横截面积,R为电阻值.
解答 解:原来的电阻为:R=ρ$\frac{L}{S}$;
把其中的一根的长度均匀拉伸到原来的4倍,截面积减小为原来的$\frac{1}{2}$,故:R拉=ρ$\frac{2L}{\frac{S}{2}}$=4ρ$\frac{L}{S}$=4R;
把另一根导线对折后并接起来,长度变为原来的一半,截面积增加为2倍,故:R并=ρ $\frac{\frac{L}{2}}{2S}$=$\frac{1}{4}$ρ$\frac{L}{S}$=$\frac{1}{4}$R;
故R拉:R并=16:1
答:它们的电阻之比为16:1.
点评 本题关键明确导线体积不变,拉长截面积减小,对折截面积变大,然后根据电阻定律列式分析.

练习册系列答案
相关题目
18. 如图是某一种手机电池铭牌,该电池用于手机待机时间约50小时,若该手机在待机时间内总体看成是正常工作,则以下关于它的额定功率P的算法正确的是( )
如图是某一种手机电池铭牌,该电池用于手机待机时间约50小时,若该手机在待机时间内总体看成是正常工作,则以下关于它的额定功率P的算法正确的是( )
 如图是某一种手机电池铭牌,该电池用于手机待机时间约50小时,若该手机在待机时间内总体看成是正常工作,则以下关于它的额定功率P的算法正确的是( )
如图是某一种手机电池铭牌,该电池用于手机待机时间约50小时,若该手机在待机时间内总体看成是正常工作,则以下关于它的额定功率P的算法正确的是( )| A. | P=3.6×750=2700W | B. | P=3.6×750×10-3=2.7W | ||
| C. | P=4.2×750=3150W | D. | P=4.2×750×10-3=3.15W |
2.磁性材料已经广泛的用在我们的生活之中,下列器件中,没有应用磁性材料的是( )
| A. | 录像带 | B. | 录音带 | C. | VCD光盘 | D. | 存储软盘 |
12.一个物体受到三个力的作用而做匀速直线运动,已知其中两个力的大小分别为12N和8N,则第三个力的大小可能为( )
| A. | 2N | B. | 3N | C. | 20N | D. | 30N |
19.台球以10m/s的速度沿与框边垂直的方向撞击后以8m/s的速度反向弹回.若球与框边的接触时间为0.1s,则台球在与边框碰撞的过程中,它的平均加速度大小和方向为( )
| A. | 20m/s2沿球弹回的方向 | B. | 20m/s2沿球撞击的方向 | ||
| C. | 180m/s2 沿球弹回的方向 | D. | 180m/s2 沿球撞击的方向 |
16.如图,在匀强电场中,把一正电荷从A点移至B点的过程中,则( )


| A. | 所受的电场力不变 | B. | 所受的电场力变大 | ||
| C. | 正电荷的电势能不变 | D. | 正电荷的电势能变大 |
17.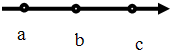 如图所示,a、b、c为一条电场线上的三个点,ab=bc 下列关于各电势 φ和场强E的比较,正确的是( )
如图所示,a、b、c为一条电场线上的三个点,ab=bc 下列关于各电势 φ和场强E的比较,正确的是( )
 如图所示,a、b、c为一条电场线上的三个点,ab=bc 下列关于各电势 φ和场强E的比较,正确的是( )
如图所示,a、b、c为一条电场线上的三个点,ab=bc 下列关于各电势 φ和场强E的比较,正确的是( )| A. | φa>φb>φc | B. | Ea>Eb>Ec | C. | Φa-φb=φb-φc | D. | Ea=Eb=Ec |
 有一远距离输电系统,A地有一台升压变压器,B地有一台匝数比为10:1的降压变压器,降压变压器副线圈上的电流为100A,输出功率是12kW,A、B两地输电线的总电阻是20Ω,求:
有一远距离输电系统,A地有一台升压变压器,B地有一台匝数比为10:1的降压变压器,降压变压器副线圈上的电流为100A,输出功率是12kW,A、B两地输电线的总电阻是20Ω,求: