Question

【题目】如图所示,传送带以v=10m/s速度向左匀速运行,AB段长L为2m,竖直平面内的光滑半圆形圆弧槽在B点与水平传送带相切,半圆弧的直径BD=3.2m且B、D连线恰好在竖直方向上,质量m为0.2kg的小滑块与传送带间的动摩擦因数μ为0.5,g取10m/s2,不计小滑块通过连接处的能量损失.图中OM连线与水平半径OC连线夹角为300求:

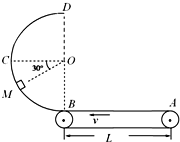
(1)小滑块从M处无初速度滑下,到达底端B时的速度;

(2)小滑块从M处无初速度滑下后,在传送带上向右运动的最大距离以及此过程产生的热量;

(3)将小滑块无初速度的放在传送带的A端,要使小滑块能通过半圆弧的最高点D,传送带AB段至少为多长?

Answer 1

【答案】（1）4m/s（2）1.6m；9.6J（3）8m

【解析】

（1）根据机械能守恒定律求出小滑块到达底端B时的速度大小．
（2）根据牛顿第二定律求出匀减速运动的加速度，结合速度位移公式求出滑块在传送带上向右运动的最大距离，结合运动学公式求出发生的相对路程大小，结合Q=Ffx相求出产生的热量．
（3）根据牛顿第二定律求出最高点的最小速度，根据机械能守恒定律求出B点的速度，结合速度位移公式求出传送带的至少长度．

（1）根据机械能守恒定律：mgR（1-cos60°）=mvB2
代入数据解得：vB=4m/s．
（2）小滑块做匀减速运动至速度为零时距离最大，有：
0-vB2=-2ax
匀减速运动的加速度大小为：a=μg=5m/s2
代入数据解得：x=1.6m
匀减速运动的时间为：

滑块与传送带之间的相对路程为：x相=vt+vBt=10×0.8+×4×0.8=9.6m
则产生的热量为：Q=Ffx相=μmgx相=0.5×2×9.6J=9.6J．
（3）小滑块能通过N点的临界条件：mg=m
解得vD＝＝4m/s
根据机械能守恒关系：-mg2R=mvD2mvB′2
代入数据解得：vB′=4m/s
小滑块在传送带上加速过程：vB′2=2ax′ ．