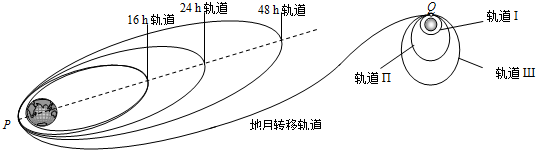
题目内容
“嫦娥一号”在距离月球表面高为h处绕月球作匀速圆周运动,已知月球半径为R,月球表面的重力加速度为g,求:“嫦娥一号”环绕月球运行的周期为多少?
【答案】分析:根据绕月卫星的万有引力等于向心力和月球表面重力等于万有引力,联立列式求解出周期;
解答:解:(1)绕月卫星绕月球做匀速圆周运动,根据万有引力提供向心力,设卫星的质量为m、轨道半径为r、月球质量为M,有
G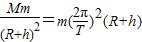
地球表面重力加速度公式
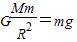
联立①②得到
T=2π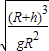
答:“嫦娥一号”环绕月球运行的周期为T=2π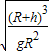
点评:本题关键根据绕月卫星受到的万有引力等于向心力,以及近月卫星和近地卫星受到的重力等于向心力列式计算.
解答:解:(1)绕月卫星绕月球做匀速圆周运动,根据万有引力提供向心力,设卫星的质量为m、轨道半径为r、月球质量为M,有
G
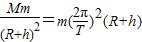
地球表面重力加速度公式
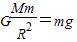
联立①②得到
T=2π
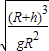
答:“嫦娥一号”环绕月球运行的周期为T=2π
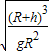
点评:本题关键根据绕月卫星受到的万有引力等于向心力,以及近月卫星和近地卫星受到的重力等于向心力列式计算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目