题目内容
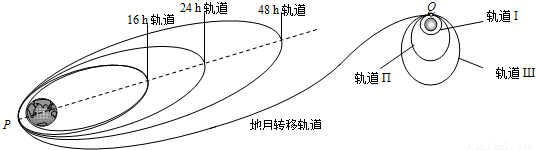
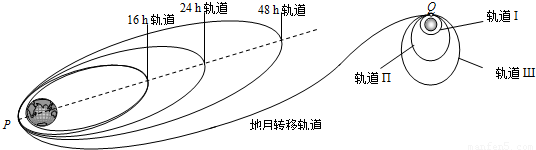
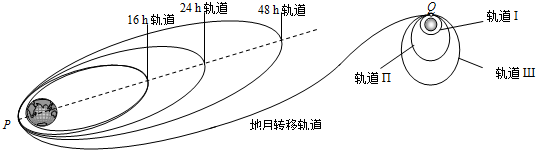
如图所示为我国“嫦娥一号卫星”从发射到进入月球工作轨道的过程示意图.在发射过程中,经过一系列的加速和变轨,卫星沿绕地球“48小时轨道”在抵达近地点P时,主发动机启动,“嫦娥一号卫星”的速度在很短时间内由v1提高到v2,进入“地月转移轨道”,开始了从地球向月球的飞越.“嫦娥一号卫星”在“地月转移轨道”上经过114小时飞行到达近月点Q时,需要及时制动,使其成为月球卫星.之后,又在绕月球轨道上的近月点Q经过两次制动,最终进入绕月球的圆形工作轨道I.已知“嫦娥一号卫星”质量为m0,在绕月球的圆形工作轨道I上运动的周期为T,月球的半径r月,月球的质量为m月,万有引力恒量为G.
(1)求卫星从“48小时轨道”的近地点P进入“地月转移轨道”过程中主发动机对“嫦娥一号卫星”做的功(不计地球引力做功和卫星质量变化);
(2)求“嫦娥一号卫星”在绕月球圆形工作轨道?运动时距月球表面的高度;
(3)理论证明,质量为m的物体由距月球无限远处无初速释放,它在月球引力的作用下运动至距月球中心为r处的过程中,月球引力对物体所做的功可表示为W=Gm月m/r.为使“嫦娥一号卫星”在近月点Q进行第一次制动后能成为月球的卫星,且与月球表面的距离不小于圆形工作轨道?的高度,最终进入圆形工作轨道,其第一次制动后的速度大小应满足什么条件?
(1)求卫星从“48小时轨道”的近地点P进入“地月转移轨道”过程中主发动机对“嫦娥一号卫星”做的功(不计地球引力做功和卫星质量变化);
(2)求“嫦娥一号卫星”在绕月球圆形工作轨道?运动时距月球表面的高度;
(3)理论证明,质量为m的物体由距月球无限远处无初速释放,它在月球引力的作用下运动至距月球中心为r处的过程中,月球引力对物体所做的功可表示为W=Gm月m/r.为使“嫦娥一号卫星”在近月点Q进行第一次制动后能成为月球的卫星,且与月球表面的距离不小于圆形工作轨道?的高度,最终进入圆形工作轨道,其第一次制动后的速度大小应满足什么条件?

分析:(1)根据动能定理,主发动机在嫦娥一号卫星进入地月转移轨道过程中对卫星做的功W=
m0v22-
m0v12
(2)设“嫦娥一号卫星”在圆轨道?上运动时距月球表面的高度为h,根据万有引力定律和向心力公式有G
=m0(r月+h)
,化简即可算出h.
(3)设“嫦娥一号卫星”在近月点进行第一次制动后,在圆轨道?上运动的速度为u1,则u1=
,代入上面h的值,化简可达到u1.
设“嫦娥一号卫星”在通过近月点脱离月球引力束缚飞离月球的速度为u2,根据机械能守恒定律
m0u22-G
=0,可解得u2.
所以,“嫦娥一号卫星”在近月点进行第一次制动后的速度u应满足的条件是:u1<u<u2.
| 1 |
| 2 |
| 1 |
| 2 |
(2)设“嫦娥一号卫星”在圆轨道?上运动时距月球表面的高度为h,根据万有引力定律和向心力公式有G
| m月m0 |
| (r月+h)2 |
| 4π2 |
| T2 |
(3)设“嫦娥一号卫星”在近月点进行第一次制动后,在圆轨道?上运动的速度为u1,则u1=
| 2π(r月+h) |
| T |
设“嫦娥一号卫星”在通过近月点脱离月球引力束缚飞离月球的速度为u2,根据机械能守恒定律
| 1 |
| 2 |
| m月m0 |
| r月+h |
所以,“嫦娥一号卫星”在近月点进行第一次制动后的速度u应满足的条件是:u1<u<u2.
解答:解:(1)根据动能定理,主发动机在嫦娥一号卫星进入地月转移轨道过程中对卫星做的功W=
m0v22-
m0v12
(2)设“嫦娥一号卫星”在圆轨道?上运动时距月球表面的高度为h,根据万有引力定律和向心力公式有
G
=m0(r月+h)
解得:h=
-r月
(3)设“嫦娥一号卫星”在近月点进行第一次制动后,在圆轨道?上运动的速度为u1,则
u1=
解得:u1=
设“嫦娥一号卫星”在通过近月点脱离月球引力束缚飞离月球的速度为u2,根据机械能守恒定律
m0u22-G
=0
解得:u2=
所以,“嫦娥一号卫星”在近月点进行第一次制动后的速度u应满足的条件是:
<u<
答:(1)卫星从“48小时轨道”的近地点P进入“地月转移轨道”过程中主发动机对“嫦娥一号卫星”做的功W=
m0v22-
m0v12.
(2)“嫦娥一号卫星”在绕月球圆形工作轨道?运动时距月球表面的高度h=
-r月.
(3)理论证明,质量为m的物体由距月球无限远处无初速释放,它在月球引力的作用下运动至距月球中心为r处的过程中,月球引力对物体所做的功可表示为W=Gm月m/r.为使“嫦娥一号卫星”在近月点Q进行第一次制动后能成为月球的卫星,且与月球表面的距离不小于圆形工作轨道?的高度,最终进入圆形工作轨道,其第一次制动后的速度大小应满足:
<u<
.
| 1 |
| 2 |
| 1 |
| 2 |
(2)设“嫦娥一号卫星”在圆轨道?上运动时距月球表面的高度为h,根据万有引力定律和向心力公式有
G
| m月m0 |
| (r月+h)2 |
| 4π2 |
| T2 |
解得:h=
| 3 |
| ||
(3)设“嫦娥一号卫星”在近月点进行第一次制动后,在圆轨道?上运动的速度为u1,则
u1=
| 2π(r月+h) |
| T |
解得:u1=
| 3 |
| ||
设“嫦娥一号卫星”在通过近月点脱离月球引力束缚飞离月球的速度为u2,根据机械能守恒定律
| 1 |
| 2 |
| m月m0 |
| r月+h |
解得:u2=
| 2 |
| 3 |
| ||
所以,“嫦娥一号卫星”在近月点进行第一次制动后的速度u应满足的条件是:
| 3 |
| ||
| 2 |
| 3 |
| ||
答:(1)卫星从“48小时轨道”的近地点P进入“地月转移轨道”过程中主发动机对“嫦娥一号卫星”做的功W=
| 1 |
| 2 |
| 1 |
| 2 |
(2)“嫦娥一号卫星”在绕月球圆形工作轨道?运动时距月球表面的高度h=
| 3 |
| ||
(3)理论证明,质量为m的物体由距月球无限远处无初速释放,它在月球引力的作用下运动至距月球中心为r处的过程中,月球引力对物体所做的功可表示为W=Gm月m/r.为使“嫦娥一号卫星”在近月点Q进行第一次制动后能成为月球的卫星,且与月球表面的距离不小于圆形工作轨道?的高度,最终进入圆形工作轨道,其第一次制动后的速度大小应满足:
| 3 |
| ||
| 2 |
| 3 |
| ||
点评:抓住解题的关键,(1)地球表面万有引力等于重力,(2)万有引力提供卫星绕地球圆周运动的向心力.外力对外星做的功等于卫星轨道转移过程中的动能的变化.

练习册系列答案
相关题目
如图所示为我国“嫦娥一号”卫星从发射到进入月球工作轨道的过程示意图.在发射过程中,经过一系列的加速和变轨,卫星沿绕地球“48小时轨道”在抵达近地点P时,主发动机启动,“嫦娥一号”卫星的速度在很短时间内由v1提高到v2,进入“地月转移轨道”,开始了从地球向月球的飞越.“嫦娥一号”卫星在“地月转移轨道”上经过114小时飞行到达近月点Q时,需要及时制动,使其成为月球卫星.之后,又在绕月球轨道上的近月点Q经过两次制动,最终进入绕月球的圆形工作轨道I.已知“嫦娥一号”卫星质量为m0,在绕月球的圆形工作轨道I上运动的周期为T,月球的半径r月,月球的质量为m月,万有引力恒量为G.
 |
(1)求卫星从“48小时轨道”的近地点P进入”地月转移轨道”过程中主发动机对“嫦娥一号”卫星做的功(不计地球引力做功和卫星质量变化);
(2)求“嫦娥一号”卫星在绕月球圆形工作轨道I运动时距月球表面的高度;
(3)理论证明,质量为m的物体由距月球无限远处无初速释放,它在月球引力的作用下运动至距月球中心为r处的过程中,月球引力对物体所做的功可表示为W= G![]() .为使“嫦娥一号”卫星在近月点Q进行第一次制动后能成为月球的卫星,且与月球表面的距离不小于圆形工作轨道I的高度,最终进入圆形工作轨道,其第一次制动后的速度大小应满足什么条件?
.为使“嫦娥一号”卫星在近月点Q进行第一次制动后能成为月球的卫星,且与月球表面的距离不小于圆形工作轨道I的高度,最终进入圆形工作轨道,其第一次制动后的速度大小应满足什么条件?