题目内容
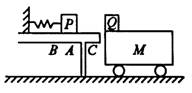
 水平放置的轻弹簧左端固定,小物块P(可视为质点)置于水平桌面的A点并与弹簧的右端接触但不相连,此时弹簧处于原长,现用力缓慢地向左水平推P至B点(弹簧仍在弹性限度内),推力做的功是6 J,撤去推力后,P沿桌面滑到一辆停在光滑水面地面、紧靠水平桌边缘的平板小车Q上,小车的上表面与桌面在同一水平面上,已知P的质量为m=1kg,Q的质量为M=4kg,A、B间距L1=20 cm,A离桌边沿C的距离L2=60cm,P与桌面间的动摩擦因数为μ1=0.4,g=10m/s2,物块P滑出小车Q时的速度v1=0.8m/s,小车Q长L3=50 cm.求:
水平放置的轻弹簧左端固定,小物块P(可视为质点)置于水平桌面的A点并与弹簧的右端接触但不相连,此时弹簧处于原长,现用力缓慢地向左水平推P至B点(弹簧仍在弹性限度内),推力做的功是6 J,撤去推力后,P沿桌面滑到一辆停在光滑水面地面、紧靠水平桌边缘的平板小车Q上,小车的上表面与桌面在同一水平面上,已知P的质量为m=1kg,Q的质量为M=4kg,A、B间距L1=20 cm,A离桌边沿C的距离L2=60cm,P与桌面间的动摩擦因数为μ1=0.4,g=10m/s2,物块P滑出小车Q时的速度v1=0.8m/s,小车Q长L3=50 cm.求:(1)小物块P在桌边沿C的速度大小vC=?
(2)小物块P与小车Q上表面间的动摩擦因数μ2=?
(3)小物块P在小车上表面上运动的过程中,小车通过的距离?
分析:(1)对A到B再到C过程,运用动能定理求出小物块P在桌边沿的速度大小.
(2)物块在滑上小车的过程中,动量守恒,根据动量守恒定律求出物块滑出小车后小车的速度,根据摩擦产生的内能等于系统损失的动能求出动摩擦因数.
(3)根据牛顿第二定律求出小车的加速度,再根据速度位移公式求出小车运动的位移.
(2)物块在滑上小车的过程中,动量守恒,根据动量守恒定律求出物块滑出小车后小车的速度,根据摩擦产生的内能等于系统损失的动能求出动摩擦因数.
(3)根据牛顿第二定律求出小车的加速度,再根据速度位移公式求出小车运动的位移.
解答:解:(1)滑块在从A到B、B到A、A到C的整个过程中,设弹簧做功为W1,外力做功为W2,摩擦力做功为W3,则
W1=0,W2=6J,W3=-μ1mg(L1+L1+L2)=-4 J
根据功能关系有:
W1+W2+W3=
mvc2-0
解得vc=2 m/s
(2)设物块滑出小车后小车的速度为v2,根据动量守恒定律
mvc=mv1+Mv2
解得v2=0.3m/s
由能量守恒得μ2mgL3=
mvc2-
mv12-
Mv22
解得μ2=0.3
(3)设小车的加速度为a,通过的距离为l,则
a=
=0.75m/s2
由v22=2aL
得L=
=0.06m.
答:(1)小物块P在桌边沿C的速度大小为2m/s.
(2)小物块P与小车Q上表面间的动摩擦因数为0.3.
(3)小物块P在小车上表面上运动的过程中,小车通过的距离为0.06m.
W1=0,W2=6J,W3=-μ1mg(L1+L1+L2)=-4 J
根据功能关系有:
W1+W2+W3=
| 1 |
| 2 |
解得vc=2 m/s
(2)设物块滑出小车后小车的速度为v2,根据动量守恒定律
mvc=mv1+Mv2
解得v2=0.3m/s
由能量守恒得μ2mgL3=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得μ2=0.3
(3)设小车的加速度为a,通过的距离为l,则
a=
| μ2mg |
| M |
由v22=2aL
得L=
| v22 |
| 2a |
答:(1)小物块P在桌边沿C的速度大小为2m/s.
(2)小物块P与小车Q上表面间的动摩擦因数为0.3.
(3)小物块P在小车上表面上运动的过程中,小车通过的距离为0.06m.
点评:本题综合考查了动能定理、动量守恒定律以及能量守恒定律,综合性较强,对学生的能力要求较高,关键需理清运动过程,选择合适的规律进行求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
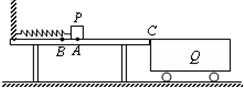
 如图所示,水平放置的轻弹簧左端固定,小物块P置于光滑水平桌面上的A点并与弹簧的右端接触且不粘连,此时弹簧处于原长.现用水平向左的推力将P缓慢推至B点(弹簧仍在弹性限度内)时,推力做的功为WF=8J.撤去推力后,P沿桌面滑到停在光滑水平面的平板小车Q上,小车的上表面与桌面在同一水平面上.已知P、Q质量分别为m=1Kg、M=4Kg,P与Q的动摩擦因数为μ=0.4.取g=10m/s2,求:
如图所示,水平放置的轻弹簧左端固定,小物块P置于光滑水平桌面上的A点并与弹簧的右端接触且不粘连,此时弹簧处于原长.现用水平向左的推力将P缓慢推至B点(弹簧仍在弹性限度内)时,推力做的功为WF=8J.撤去推力后,P沿桌面滑到停在光滑水平面的平板小车Q上,小车的上表面与桌面在同一水平面上.已知P、Q质量分别为m=1Kg、M=4Kg,P与Q的动摩擦因数为μ=0.4.取g=10m/s2,求: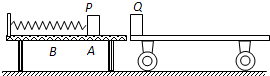 如图所示,质量M=1.5kg的小车静止于光滑水平面上并靠近固定在水平面上的桌子右边,其上表面与水平桌面相平,小车的左端放有一质量为0.5kg的滑块Q.水平放置的轻弹簧左端固定,质量为0.5kg的小物块P置于桌面上的A点并与弹簧的右端接触,此时弹簧处于原长.现用水平向左的推力将P缓慢推至B点(弹簧仍在弹性限度内)时,推力做的功为WF=4J,撤去推力后,P沿光滑的桌面滑到小车左端并与Q发生弹性碰撞,最后Q恰好没从小车上滑下.已知Q与小车表面间动摩擦因数μ2=0.1.(g=10m/s2)
如图所示,质量M=1.5kg的小车静止于光滑水平面上并靠近固定在水平面上的桌子右边,其上表面与水平桌面相平,小车的左端放有一质量为0.5kg的滑块Q.水平放置的轻弹簧左端固定,质量为0.5kg的小物块P置于桌面上的A点并与弹簧的右端接触,此时弹簧处于原长.现用水平向左的推力将P缓慢推至B点(弹簧仍在弹性限度内)时,推力做的功为WF=4J,撤去推力后,P沿光滑的桌面滑到小车左端并与Q发生弹性碰撞,最后Q恰好没从小车上滑下.已知Q与小车表面间动摩擦因数μ2=0.1.(g=10m/s2)