题目内容
【题目】如图所示,在竖直平面的xOy坐标系中,Oy竖直向上,Ox水平。设平面内存在沿x轴正方向的恒定风力。一小球从坐标原点沿Oy方向竖直向上抛出,初速度为v0=4m/s,不计空气阻力,到达最高点的位置如图中M点所示,(坐标格为正方形,g=10m/s2)求:
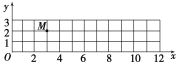
(1)小球在M点的速度v1;
(2)在图中定性画出小球的运动轨迹并标出小球落回x轴时的位置N;
(3)小球到达N点的速度v2的大小。
【答案】(1)6 m/s (2) 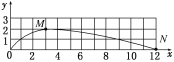 (3)
(3) ![]() m/s
m/s
【解析】
试题(1)设正方形的边长为![]() ,竖直方向做竖直上抛运动,
,竖直方向做竖直上抛运动,![]() ,
,![]() ,水平方向做匀加速直线运动,
,水平方向做匀加速直线运动,![]() ,解得
,解得![]() 。
。
(2)由竖直方向的对称性可知,小球再经过![]() 到
到![]() 轴,水平方向做初速度为零的匀加速直线运动,所以回到x轴时落到
轴,水平方向做初速度为零的匀加速直线运动,所以回到x轴时落到![]() 处,位置N的坐标为(12,0)。
处,位置N的坐标为(12,0)。
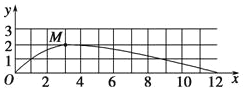
(3)物体从O到M的时间与M到N的时间相等,因此此运动可看成水平方向做初速度为零的匀加速直线运动,竖直方向可看成竖直上抛运动,所以物体到达N点水平方向的速度为v,则![]() ,所以
,所以![]() ,而竖直方向N点的速度为
,而竖直方向N点的速度为![]() ,那么N点的速度为
,那么N点的速度为![]() 。
。

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目