Question

【题目】如图所示，倾角为α的光滑斜面与半径为R＝0.4 m半圆形光滑轨道在同一竖直平面内，其中斜面与水平面BE光滑连接，水平面BE长为L＝0.4 m，直径CD沿竖直方向，C、E可看做重合。现有一可视为质点的小球从斜面上距B点竖直距离为H的地方由静止释放，小球在水平面上所受阻力为其重力的。(取g＝10 m/s2)求：

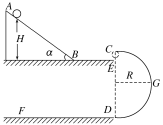
（1）若要使小球经E处水平进入圆形轨道且能沿轨道运动，H至少要有多高？

（2）如小球恰能沿轨道运动，那么小球在水平面DF上能滑行多远？

Answer 1

【答案】（1） （2）5m

【解析】

(1)小球从光滑斜面轨道下滑，机械能守恒，设到达B点时的速度大小为v，则

mgH＝mv2

因为小球在水平面所受阻力为其重力的，

根据牛顿第二定律a＝＝2 m/s2。

vE2－v2＝－2aL

小球能在竖直平面内做圆周运动，在圆形轨道最高点必须满足：

mg≤m

联立以上几式并代入数据得：H≥0.28 m

小球恰能沿轨道运动，则在E点应该有

根据动能定理：

mg·2R－kmg·x＝0－mvE2，

代入数据可解得：x＝5 m。

故本题答案是：（1） （2）5m