题目内容
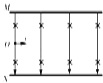
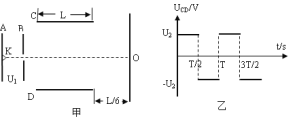
【题目】如图所示，真空室中电极K发出的电子(初速不计）经过电势差为U1的加速电场加速后，沿两水平金属板C、D间的中心线射入两板间的偏转电场，最后打在荧光屏上。CD两板间的电势差UCD随时间变化如图所示，设C、D间的电场可看作是均匀的，且两板外无电场。已知电子的质量为m、电荷量为e(重力不计)，C、D极板长为L, 板间距离为d,偏转电压U2,荧光屏距C、D右端的距离为L/6, 不同时刻从K极射出的电子都能通过偏转电极且不计电子间的相互作用。求：
（1）电子通过偏转电场的时间t0
（2）若UCD的周期T=t0, 荧光屏上电子能够到达的区域的长度；
（3）若UCD的周期T=2t0, 到达荧光屏上O点的电子的动能？
【答案】（1）
（2）
（3）
【解析】
（1）电子先AB板间电场加速，后进入CD板间电场偏转做类平抛运动，最后离开电场而做匀速直线运动．先由动能定理求出加速获得的速度．电子在偏转电场中，水平方向做匀速直线运动，由公式
求时间；（2）当
时，所有电子在偏转电场中运动过程，竖直方向加速半个周期，减速半个周期，最终水平飞出射出电场。t=0时刻进入的电子向上侧移距离最大．根据牛顿第二定律和运动学公式结合求出最大的偏转距离，向下偏转的最大距离等于向上偏转的最大距离。即可得到荧光屏上电子能够到达的区域的长度；（3）当
时，电子要到达O点必须在竖直方向有先加速后减速再反向加速过程，并且加速大小相等，整个过程向上的位移和向下的位移大小相等，根据位移相等，由运动学公式求出向上加速的时间，求得竖直方向偏转的距离，根据动能定理求解到达荧光屏上O点的电子的动能。
（1）电子在电场中加速过程：
在偏转电场中运动，水平方向做匀速运动：
联立解得：
（2）当时，所有电子在偏转电场中运动过程，竖直方向加速半个周期，减速半个周期，最终水平飞出．由竖直方向速度时间图象得，
时刻进入的电子向上侧移距离最大。
同理得向下侧移距离最大值：
所以电子达到的区域长：
（3）当时，电子要到达O点必须在竖直方向有先加速后减速再反向加速过程，并且加速大小相等，整个过程向上的位移和向下的位移大小相等，设向上加速时间为△t，加速度大小为a，
则在竖直方向上有：
要到达O点，
联立解得：
所以到达O点的电子经过偏转电场时电子做功，
电子从K到O过程由动能定理得：
