题目内容
19.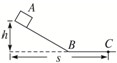 如图所示,一物体在高h的斜面上从静止开始下滑,滑到平面上的C点静止下来,不计物块在交接点的能量损失,且AC水平距离为s,设物块与斜面和平面的动摩擦因数相同,则该动摩擦因数大小为$\frac{h}{s}$.
如图所示,一物体在高h的斜面上从静止开始下滑,滑到平面上的C点静止下来,不计物块在交接点的能量损失,且AC水平距离为s,设物块与斜面和平面的动摩擦因数相同,则该动摩擦因数大小为$\frac{h}{s}$.
分析 本题可将全过程使用动能定理求解,注意物体沿斜面下滑过程中,克服摩擦力做的功只与斜面底边长决定.
解答 解:设AB与水平面的夹角为θ,对物体全过程应用动能定理,有:
mgh-μmgcosθ•$\frac{h}{sinθ}$-$μmg(s-\frac{h}{tanθ})$=0,
解得:μ=$\frac{h}{s}$.
故答案为:$\frac{h}{s}$
点评 要熟记结论:物体沿斜面运动过程中克服摩擦力做的功等于动摩擦因数、重力、斜面底边长三者的乘积.

练习册系列答案
相关题目
9.如图所示,光滑斜面AE被分成四个相等的部分,一物体由A点从静止释放,则( )


| A. | 物体到达各点的速率vB:vC:vD:vE=1:2:3:4 | |
| B. | 物体到达各点所经历的时间tB:tC:tD:tE=1:($\sqrt{2}$-1):($\sqrt{3}$-$\sqrt{2}$):(2-$\sqrt{3}$) | |
| C. | 物体从A到E的平均速度等于B点的瞬时速度 | |
| D. | 物体通过每一部分时,其速度增量vB-vA=vC-vB=vE-vD |
7.有一毫安表,它的内阻是100Ω,量程为2mA,现要将它改装成量程为10A的电流表,则毫安表应( )
| A. | 并联一个0.02Ω的电阻 | B. | 并联一个0.2Ω的电阻 | ||
| C. | 串联一个50Ω的电阻 | D. | 串联一个4900Ω的电阻 |
4.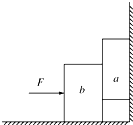 物体b在力F作用下将物体a压向光滑的竖直墙壁,a始终处于静止状态.如图所示,当F逐渐增大时则下列说法中正确的是( )
物体b在力F作用下将物体a压向光滑的竖直墙壁,a始终处于静止状态.如图所示,当F逐渐增大时则下列说法中正确的是( )
 物体b在力F作用下将物体a压向光滑的竖直墙壁,a始终处于静止状态.如图所示,当F逐渐增大时则下列说法中正确的是( )
物体b在力F作用下将物体a压向光滑的竖直墙壁,a始终处于静止状态.如图所示,当F逐渐增大时则下列说法中正确的是( )| A. | a受的摩擦力有两个 | |
| B. | a与b间的最大摩擦力大小随F的增大而增大 | |
| C. | a受的摩擦力大小不随F的增大而变化 | |
| D. | b相对a的运动趋势方向竖直向下 |
8.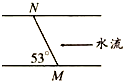 如图所示,在一段河岸平直的河中,一船夫划小船由M点出发沿直线到达对岸N点,直线MN与河岸成53°角.已知河宽为48m.河中水流的速度大小为v=5.0m/s,船夫划船在静水中的速度大小为5.0m/s,则小船过河的时间为(sin53°=0.8)( )
如图所示,在一段河岸平直的河中,一船夫划小船由M点出发沿直线到达对岸N点,直线MN与河岸成53°角.已知河宽为48m.河中水流的速度大小为v=5.0m/s,船夫划船在静水中的速度大小为5.0m/s,则小船过河的时间为(sin53°=0.8)( )
 如图所示,在一段河岸平直的河中,一船夫划小船由M点出发沿直线到达对岸N点,直线MN与河岸成53°角.已知河宽为48m.河中水流的速度大小为v=5.0m/s,船夫划船在静水中的速度大小为5.0m/s,则小船过河的时间为(sin53°=0.8)( )
如图所示,在一段河岸平直的河中,一船夫划小船由M点出发沿直线到达对岸N点,直线MN与河岸成53°角.已知河宽为48m.河中水流的速度大小为v=5.0m/s,船夫划船在静水中的速度大小为5.0m/s,则小船过河的时间为(sin53°=0.8)( )| A. | 4.8s | B. | l0s | C. | 14.4s | D. | 20s |
9.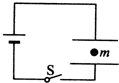 图中两板间距为d的平行板电容器与一电源连接,电健s闭合,电容器两板间有一质量为m,电量为q的微粒静止不动,下列说法中正确的是( )
图中两板间距为d的平行板电容器与一电源连接,电健s闭合,电容器两板间有一质量为m,电量为q的微粒静止不动,下列说法中正确的是( )
 图中两板间距为d的平行板电容器与一电源连接,电健s闭合,电容器两板间有一质量为m,电量为q的微粒静止不动,下列说法中正确的是( )
图中两板间距为d的平行板电容器与一电源连接,电健s闭合,电容器两板间有一质量为m,电量为q的微粒静止不动,下列说法中正确的是( )| A. | 微粒带正电 | |
| B. | 增大电容器两极板间距离,微粒向下运动 | |
| C. | 电源两端电压为mgd/q | |
| D. | 断开电键s,微粒向下运动 |
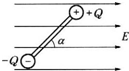 如图所示,一根绝缘杆长l,两端分别带有等量异号电荷,电荷量为Q,杆处于纸面内时,匀强电场的方向与杆的方向成角度α=60°,若场强为E,使杆沿顺时针方向转过60°角时,电场力一共做了多少功?其中负电荷的电势能有什么变化?变化了多少?
如图所示,一根绝缘杆长l,两端分别带有等量异号电荷,电荷量为Q,杆处于纸面内时,匀强电场的方向与杆的方向成角度α=60°,若场强为E,使杆沿顺时针方向转过60°角时,电场力一共做了多少功?其中负电荷的电势能有什么变化?变化了多少?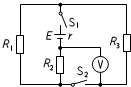 如图所示电路中,电阻R1=R2=R3=10Ω,电源内阻r=5Ω,电压表可视为理想电表.当开关S1和S2均闭合时,电压表的示数为10V.求
如图所示电路中,电阻R1=R2=R3=10Ω,电源内阻r=5Ω,电压表可视为理想电表.当开关S1和S2均闭合时,电压表的示数为10V.求