Question

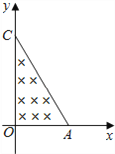
【题目】如图，A、C两点分别位于x轴和y轴上，∠OCA=30°，OA的长度为L．在△OCA区域内有垂直于xOy平面向里的匀强磁场．质量为m、电荷量为q的带正电粒子，以平行于y轴的方向从OA边射入磁场．已知粒子从某点射入时，恰好垂直于OC边射出磁场，且粒子在磁场中运动的时间为t0．不计重力．

（1）求磁场的磁感应强度的大小；

（2）若粒子先后从两不同点以相同的速度射入磁场，恰好从OC边上的同一点射出磁场，求该粒子这两次在磁场中运动的时间之和；

（3）若粒子从某点射入磁场后，其运动轨迹与AC边相切，且在磁场内运动的时间为，求粒子此次入射速度的大小.

Answer 1

【答案】(1) ；(2) ；(3)

【解析】试题分析：(1)粒子垂直OA进入磁场中，转过90°，垂直打在y轴上，则，求出周期，由周期公式，求B的大小

(2)画出两个粒子的运动轨迹，设轨迹所对应的圆心角分别为和，由几何关系有，可得到时间之和等于；

(3) 根据圆周运动知识知道，两粒子在磁场中运动的时间差与成正比，只要求出的最大值，即可求得的最大值。

（1）粒子在磁场中做匀速圆周运动，在时间t0内其速度方向改变了90°，故其周期

T=4t0①

设磁感应强度大小为B，粒子速度为v，圆周运动的半径为r．由洛伦兹力公式和牛顿定律得 ②

匀速圆周运动的速度满足③

联立①②③式得 ④

（2）设粒子从OA变两个不同位置射入磁场，能从OC边上的同一点P射出磁场，粒子在磁场中运动的轨迹如图所示．

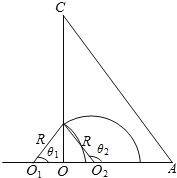
设两轨迹所对应的圆心角分别为θ1和θ2．由几何关系有

θ1=180°﹣θ2 ⑤

粒子两次在磁场中运动的时间分别为t1与t2，则

；⑥

（3）如下图，由题给条件可知，该粒子在磁场区域中的轨迹圆弧对应的圆心角为150°．

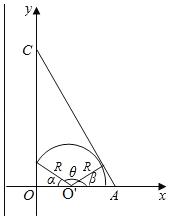
设O'为圆弧的圆心，圆弧的半径为r0，圆弧与AC相切与B点，从D点射出磁场，

由几何关系和题给条件可知，此时有

∠OO'D=∠B O'A=30°⑦

⑧

设粒子此次入射速度的大小为v0，

由圆周运动线速度公式，则有： ⑨

联立①⑦⑧⑨式得

点晴：对于带电粒子在磁场中运动类型，要善于运用几何知识帮助分析和求解，这是轨迹问题的解题关键，注意画出正确的运动轨迹图是解题的重点．