题目内容
4. 如图所示,小球沿足够长的斜面向上做匀变速运动,依次经a、b、c、d到达最高点e.已知ab=bd=6m,bc=1m,小球从a到c和从c到d所用的时间都是2s,求:
如图所示,小球沿足够长的斜面向上做匀变速运动,依次经a、b、c、d到达最高点e.已知ab=bd=6m,bc=1m,小球从a到c和从c到d所用的时间都是2s,求:(1)加速度大小;
(2)vb大小.
分析 根据连续相等时间内的位移之差是一恒量求出小球的加速度,根据某段时间内的平均速度等于中间时刻的瞬时速度求出c点的速度,根据速度位移公式求出b点的速度.
解答 解:(1)由题意知,xac=7m,xcd=5m,
根据${x}_{cd}-{x}_{ac}=a{T}^{2}$得,加速度a=$\frac{{x}_{cd}-{x}_{ac}}{{T}^{2}}=\frac{5-7}{4}m/{s}^{2}=-0.5m/{s}^{2}$.
(2)c点的瞬时速度${v}_{c}=\frac{{x}_{ac}+{x}_{cd}}{2T}=\frac{7+5}{4}m/s=3m/s$,
对bc段,根据速度位移公式得,${{v}_{c}}^{2}-{{v}_{b}}^{2}=2a{x}_{bc}$,
解得${v}_{b}=\sqrt{{{v}_{c}}^{2}-2a{x}_{bc}}=\sqrt{9+2×0.5×1}$m/s=$\sqrt{10}$m/s.
答:(1)加速度大小为0.5m/s2;
(2)vb大小为$\sqrt{10}$m/s.
点评 解决本题的关键掌握匀变速直线运动的运动学公式和推论,并能灵活运用,有时运用推论求解会使问题更加简捷.

练习册系列答案
相关题目
14.下列几组物理量中,全部为矢量的一组是( )
| A. | 时间、位移 | B. | 速度、位移 | C. | 路程、质量 | D. | 长度、路程 |
15. 如图所示,三只电压表均为理想电压表,定值电阻R1和滑动变阻器R2串联,电源内阻不能忽略.现将滑动变阻器的滑片向右移动到另一位置,发现电压表V3的示数增大了0.30V,则电压表Vl和V2的示数变化可能是( )
如图所示,三只电压表均为理想电压表,定值电阻R1和滑动变阻器R2串联,电源内阻不能忽略.现将滑动变阻器的滑片向右移动到另一位置,发现电压表V3的示数增大了0.30V,则电压表Vl和V2的示数变化可能是( )
 如图所示,三只电压表均为理想电压表,定值电阻R1和滑动变阻器R2串联,电源内阻不能忽略.现将滑动变阻器的滑片向右移动到另一位置,发现电压表V3的示数增大了0.30V,则电压表Vl和V2的示数变化可能是( )
如图所示,三只电压表均为理想电压表,定值电阻R1和滑动变阻器R2串联,电源内阻不能忽略.现将滑动变阻器的滑片向右移动到另一位置,发现电压表V3的示数增大了0.30V,则电压表Vl和V2的示数变化可能是( )| A. | V1减小0.20V,V2增大0.50V | B. | V1增大0.10V,V2增大0.20V | ||
| C. | V1减小0.10V,V2减小0.20V | D. | V1增大0.20V,V2增大0.10V |
19.北京时间2015年9月16日中午,在第34届亚奥理事会代表大会上,亚奥理事会主席艾哈迈德亲王宣布:中国杭州获得2022年亚运会主办权.而我们宁波将成为分会场,在考察下列运动员的比赛成绩时,可视为质点的是( )
| A. |  马拉松 | B. |  跳水 | C. |  击剑 | D. |  体操 |
9.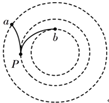 图中虚线是某电场中的一簇等势线.两个带电粒子从P点均沿等势线的切线方向射入电场,粒子运动的部分轨迹如图中实线所示.若粒子仅受电场力的作用,下列说法中正确的是( )
图中虚线是某电场中的一簇等势线.两个带电粒子从P点均沿等势线的切线方向射入电场,粒子运动的部分轨迹如图中实线所示.若粒子仅受电场力的作用,下列说法中正确的是( )
 图中虚线是某电场中的一簇等势线.两个带电粒子从P点均沿等势线的切线方向射入电场,粒子运动的部分轨迹如图中实线所示.若粒子仅受电场力的作用,下列说法中正确的是( )
图中虚线是某电场中的一簇等势线.两个带电粒子从P点均沿等势线的切线方向射入电场,粒子运动的部分轨迹如图中实线所示.若粒子仅受电场力的作用,下列说法中正确的是( )| A. | 粒子从P运动到b的过程中,动能减小 | |
| B. | a、b两点的电势关系Ua<Ub | |
| C. | 粒子从P运动到a的过程中,电势能增大 | |
| D. | a、b两点的电场强度大小关系Ea<Eb |
16.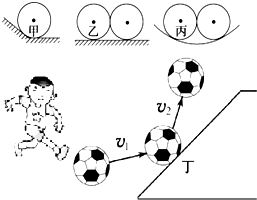 如图所示,所有的球都是相同的,且形状规则,质量分布均匀.甲球放在光滑斜面和光滑水平面之间,乙球与其右侧的球相互接触并放在光滑的水平面上,丙球与其右侧的球放在另一个大的光滑球壳内部并相互接触.一学生将丁球踢向斜台的示意图如图.关于这四个球的受力情况,下列说法正确的是( )
如图所示,所有的球都是相同的,且形状规则,质量分布均匀.甲球放在光滑斜面和光滑水平面之间,乙球与其右侧的球相互接触并放在光滑的水平面上,丙球与其右侧的球放在另一个大的光滑球壳内部并相互接触.一学生将丁球踢向斜台的示意图如图.关于这四个球的受力情况,下列说法正确的是( )
 如图所示,所有的球都是相同的,且形状规则,质量分布均匀.甲球放在光滑斜面和光滑水平面之间,乙球与其右侧的球相互接触并放在光滑的水平面上,丙球与其右侧的球放在另一个大的光滑球壳内部并相互接触.一学生将丁球踢向斜台的示意图如图.关于这四个球的受力情况,下列说法正确的是( )
如图所示,所有的球都是相同的,且形状规则,质量分布均匀.甲球放在光滑斜面和光滑水平面之间,乙球与其右侧的球相互接触并放在光滑的水平面上,丙球与其右侧的球放在另一个大的光滑球壳内部并相互接触.一学生将丁球踢向斜台的示意图如图.关于这四个球的受力情况,下列说法正确的是( )| A. | 甲球受到两个弹力的作用 | |
| B. | 乙球受到一个弹力的作用 | |
| C. | 丙球受到两个弹力的作用 | |
| D. | 丁球(足球)与斜台作用时斜台给足球的弹力方向先沿v1的方向后沿v2的方向 |
19.假设地球可视为质量均匀分布的球体,已知一颗人造地球卫星绕地球做匀速圆周运动的半径为R,周期为T;地球的半径为R0,自转周期为T0.则地球表面赤道处的重力加速度大小与两极处重力加速度大小的比值为( )
| A. | $\frac{{R_0^3{T^2}}}{{{R^3}T_0^2}}$ | B. | $\frac{{{R^3}T_0^2}}{{R_0^3{T^2}}}$ | ||
| C. | $1-\frac{{R_0^3{T^2}}}{{{R^3}T_0^2}}$ | D. | $1-\frac{{{R^3}T_0^2}}{{R_0^3{T^2}}}$ |
 如图所示,重10N的物体位于倾角θ=30°的斜面上,在沿斜面向上的F=6N的力作用下处于静止状态,则斜面对物体的摩擦力大小是多少,方向怎样?如果F分别为4N、5N.摩擦力的大小、方向又怎样?
如图所示,重10N的物体位于倾角θ=30°的斜面上,在沿斜面向上的F=6N的力作用下处于静止状态,则斜面对物体的摩擦力大小是多少,方向怎样?如果F分别为4N、5N.摩擦力的大小、方向又怎样?