题目内容
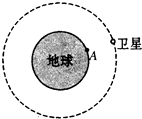 (2007?广州二模)如图所示,一颗轨道位于赤道所在平面、运行方向与地球自转方向相同的人造卫星,其圆形轨道半径为地球半径R的两倍,设地球自转的角速度为ω0,若某时刻卫星通过地面上A点的正上方,求从这时刻起到它下一次到达A点正上方所需要的时间.(已知地球表面的重力加速度为g)
(2007?广州二模)如图所示,一颗轨道位于赤道所在平面、运行方向与地球自转方向相同的人造卫星,其圆形轨道半径为地球半径R的两倍,设地球自转的角速度为ω0,若某时刻卫星通过地面上A点的正上方,求从这时刻起到它下一次到达A点正上方所需要的时间.(已知地球表面的重力加速度为g)分析:卫星绕地球做圆周运动所需要的向心力由万有引力提供G
=m?2Rω2,又有地球表面的物体G
=mg,所以有ω=
.经时间t卫星再次到达A点正上方,由运动学知识,有ωt-ω0t=2π,解出t即可.
| Mm |
| (2R)2 |
| Mm |
| R2 |
|
解答:解:设卫星绕地球做圆周运动的角速度为ω,
由万有引力定律F=G
和牛顿第二定律 F=mω2r
得G
=m?2Rω2…①
对于地球表面的物体G
=mg…②
由①、②得:ω=
…③
经时间t卫星再次到达A点正上方,由运动学知识,有ωt-ω0t=2π …④
由③、④得:t=
答:从这时刻起到它下一次到达A点正上方所需要的时间为
.
由万有引力定律F=G
| Mm |
| r2 |
和牛顿第二定律 F=mω2r
得G
| Mm |
| (2R)2 |
对于地球表面的物体G
| Mm |
| R2 |
由①、②得:ω=
|
经时间t卫星再次到达A点正上方,由运动学知识,有ωt-ω0t=2π …④
由③、④得:t=
| 4π | ||||
|
答:从这时刻起到它下一次到达A点正上方所需要的时间为
| 4π | ||||
|
点评:本题考查万有引力定律和圆周运动知识的综合应用能力.有一定的难度,属于中档题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
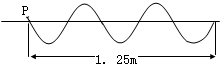 (2007?广州二模)如图所示为绳上的一列横波,某时刻的波形如图所示,绳上P点振动频率为2Hz,则此波( )
(2007?广州二模)如图所示为绳上的一列横波,某时刻的波形如图所示,绳上P点振动频率为2Hz,则此波( ) (2007?广州二模)两个物体如图放置,同时有F=1N的两个水平力分别作用于a、b上,两物体仍保持静止,则地面对物体b、物体b对物体a的摩擦力分别为( )
(2007?广州二模)两个物体如图放置,同时有F=1N的两个水平力分别作用于a、b上,两物体仍保持静止,则地面对物体b、物体b对物体a的摩擦力分别为( )