题目内容
(2007?广州二模)从水平地面上以初速度v0把小球竖直向上抛出,若小球运动中所受空气阻力是其重力的0.6倍,每次接触地面后在极短的时间内以原速率反弹,重力加速度为g求:
(1)小球从开始抛出到静止所通过的路程.
(2)小球从开始抛出到刚刚静止所经历的时间.(提示:若0<q<1,当n无穷大时,取qn=0)
(1)小球从开始抛出到静止所通过的路程.
(2)小球从开始抛出到刚刚静止所经历的时间.(提示:若0<q<1,当n无穷大时,取qn=0)
分析:(1)对从抛出到静止的整个运动过程运用动能定理列式即可求解;
(2)根据牛顿第二定律及运动学基本公式求出前三次上升和下落的时间,找出通式,对通式进行求和即可求解.
(2)根据牛顿第二定律及运动学基本公式求出前三次上升和下落的时间,找出通式,对通式进行求和即可求解.
解答:解:(1)小球最后静止在水平地面上,在整个运动过程中,空气阻力做功使其机械能减少,设小球从开始抛出到最后静止所通过的路程S,
有 fS=
m
已知 f=0.6mg 代入算得:S=
(2)第一次上升和下降:设上升的加速度为a11.上升所用的时间为t11,上升的最大高度为h1;下降的加速度为a12,下降所用时间为t12.
上升阶段:F合=mg+f=1.6 mg
由牛顿第二定律:a11=
=1.6g
根据:vt=v0-a11t11,vt=0
得:v0=l.6gt11,所以t11=
(1分)
下降阶段:a12=
=0.4g
由h1=
a11t112 和 h2=
a12t122
得:t12=2t11=
所以上升和下降所用的总时间为:T1=t11+t12=3t11=
第二次上升和下降,以后每次上升的加速度都为a11,下降的加速度都为a12;设上升的初速度为v2,上升的最大高度为h2,上升所用时间为t21,下降所用时间为t22
由v22=2a12h1和v02=2a11h1 得 v2=
v0
上升阶段:v2=a11t21 得:t21=
=
下降阶段:由 h2=
a11t212 和h2=
a12t222 得t22=2t21
所以第二次上升和下降所用总时间为:T2=t21+t22=3t21=
=
T1
第三次上升和下降,设上升的初速度为v3,上升的最大高度为h3,上升所用时间为t31,下降所用时间为t32
由 v32=2a11h2 和v22=2a12h2 得:v3=
v2=
v0
上升阶段:v3=a11t3l,得t31=
下降阶段:由 h3=
a11t312 和h3=
a12t322 得:t32=2t31
所以第三次上升和下降所用的总时间为:T3=t31+t32=3t31=
=
T1
同理,第n次上升和下降所用的总时间为:Tn=(
)n-1T1
所以,从抛出到落地所用总时间为:T=
答:(1)小球从开始抛出到静止所通过的路程为
.
(2)小球从开始抛出到刚刚静止所经历的时间为
.
有 fS=
| 1 |
| 2 |
| v | 2 0 |
已知 f=0.6mg 代入算得:S=
5
| ||
| 6g |
(2)第一次上升和下降:设上升的加速度为a11.上升所用的时间为t11,上升的最大高度为h1;下降的加速度为a12,下降所用时间为t12.
上升阶段:F合=mg+f=1.6 mg
由牛顿第二定律:a11=
| F合 |
| m |
根据:vt=v0-a11t11,vt=0
得:v0=l.6gt11,所以t11=
| 5v0 |
| 8g |
下降阶段:a12=
| mg-f |
| m |
由h1=
| 1 |
| 2 |
| 1 |
| 2 |
得:t12=2t11=
| 5v0 |
| 4g |
| 15v0 |
| 8g |
第二次上升和下降,以后每次上升的加速度都为a11,下降的加速度都为a12;设上升的初速度为v2,上升的最大高度为h2,上升所用时间为t21,下降所用时间为t22
由v22=2a12h1和v02=2a11h1 得 v2=
| 1 |
| 2 |
上升阶段:v2=a11t21 得:t21=
| v2 |
| a11 |
| 5v0 |
| 16g |
下降阶段:由 h2=
| 1 |
| 2 |
| 1 |
| 2 |
所以第二次上升和下降所用总时间为:T2=t21+t22=3t21=
| 15v0 |
| 16g |
| 1 |
| 2 |
第三次上升和下降,设上升的初速度为v3,上升的最大高度为h3,上升所用时间为t31,下降所用时间为t32
由 v32=2a11h2 和v22=2a12h2 得:v3=
| 1 |
| 2 |
| 1 |
| 4 |
上升阶段:v3=a11t3l,得t31=
| 5v0 |
| 32g |
下降阶段:由 h3=
| 1 |
| 2 |
| 1 |
| 2 |
所以第三次上升和下降所用的总时间为:T3=t31+t32=3t31=
| 15v0 |
| 32g |
| 1 |
| 4 |
同理,第n次上升和下降所用的总时间为:Tn=(
| 1 |
| 2 |
所以,从抛出到落地所用总时间为:T=
| 15v0 |
| 4g |
答:(1)小球从开始抛出到静止所通过的路程为
5
| ||
| 6g |
(2)小球从开始抛出到刚刚静止所经历的时间为
| 15v0 |
| 4g |
点评:本题主要考查了动能定理及牛顿第二定律及运动学基本公式的应用,过程较为复杂,难道适中.

练习册系列答案
相关题目
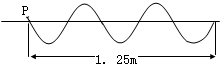 (2007?广州二模)如图所示为绳上的一列横波,某时刻的波形如图所示,绳上P点振动频率为2Hz,则此波( )
(2007?广州二模)如图所示为绳上的一列横波,某时刻的波形如图所示,绳上P点振动频率为2Hz,则此波( ) (2007?广州二模)两个物体如图放置,同时有F=1N的两个水平力分别作用于a、b上,两物体仍保持静止,则地面对物体b、物体b对物体a的摩擦力分别为( )
(2007?广州二模)两个物体如图放置,同时有F=1N的两个水平力分别作用于a、b上,两物体仍保持静止,则地面对物体b、物体b对物体a的摩擦力分别为( )