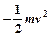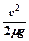题目内容
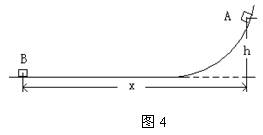
如图所示,光滑水平面MN的左端M处有一弹射装置P(P为左端固定,处于压缩状态且锁定的轻质弹簧,当A与P碰撞时P立即解除锁定),右端N处与水平传送带恰平齐且很靠近,传送带沿逆时针方向以恒定速率υ =" 5m/s" 匀速转动,水平部分长度L = 4m。放在水平面上的两相同小物块A、B(均视为质点)间有一被压缩的轻质弹簧,弹性势能Ep = 4J,弹簧与A相连接,与B不连接,A、B与传送带间的动摩擦因数μ = 0.2,物块质量mA = mB = 1kg。现将A、B由静止开始释放,弹簧弹开,在B离开弹簧时,A未与P碰撞,B未滑上传送带。取g = 10m/s2。求:
(1)B滑上传送带后,向右运动的最远处与N点间的距离sm;
(2)B从滑上传送带到返回到N端的时间t和这一过程中B与传送带间因摩擦而产生的热 能Q;
(3)B回到水平面后压缩被弹射装置P弹回的A上的弹簧,B与弹簧分离然后再滑上传 送带。则P锁定时具有的弹性势能E满足什么条件,才能使B与弹簧分离后不再与弹簧相碰。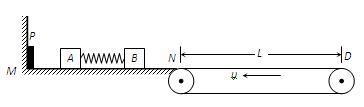
(1)B滑上传送带后,向右运动的最远处与N点间的距离sm;
(2)B从滑上传送带到返回到N端的时间t和这一过程中B与传送带间因摩擦而产生的热 能Q;
(3)B回到水平面后压缩被弹射装置P弹回的A上的弹簧,B与弹簧分离然后再滑上传 送带。则P锁定时具有的弹性势能E满足什么条件,才能使B与弹簧分离后不再与弹簧相碰。

(1)弹簧弹开的过程中,系统机械能守恒
Ep = mAυA2 + mBυB2 (1分)
由动量守恒有 mAυA- mBυB =" 0 " (1分)
联立以上两式解得 υA =" 2m/s " υB =" 2m/s " (1分)
B滑上传送带做匀减速运动,当速度减为零时,向右运动的距离最大。
由动能定理得 - μmBgsm = 0- mBυB2 (1分)
解得 sm = =" 1m " (1分)
(2)物块B先向右做匀减速运动,直到速度减小到零,然后反方向做匀加速运动, 回到皮带左端时速度大小仍为υB = 2m/s (1分)
由动量定理 - μmBgt =" -" mBυB - mBυB (1分)
解得 t = =" 2s " (1分)
B向右匀减速运动因摩擦而产生的热能为
Q1 = μmBg(υ·+ sm) (1分)
B向左匀加速运动因摩擦而产生的热能为
Q2 = μmBg(υ·- sm) (1分)
Q = Q1 + Q2 = μmBgυt = 20J (1分)
(3)设弹射装置P将A弹开时的速度为υA′,则
E = mAυA′2- mAυA2 (2分)
B离开弹簧时,AB速度互换,B的速度 υB′ = υA′ (2分)
B与弹簧分离后不再与弹簧相碰,则B滑出平台Q端,由能量关系有
mBυB′2 > μmBgL (2分)
以上三式解得
E > μmAgL- mAυA2 (2分)
代入数据解得 E> 6J (1分)
Ep = mAυA2 + mBυB2 (1分)
由动量守恒有 mAυA- mBυB =" 0 " (1分)
联立以上两式解得 υA =" 2m/s " υB =" 2m/s " (1分)
B滑上传送带做匀减速运动,当速度减为零时,向右运动的距离最大。
由动能定理得 - μmBgsm = 0- mBυB2 (1分)
解得 sm = =" 1m " (1分)
(2)物块B先向右做匀减速运动,直到速度减小到零,然后反方向做匀加速运动, 回到皮带左端时速度大小仍为υB = 2m/s (1分)
由动量定理 - μmBgt =" -" mBυB - mBυB (1分)
解得 t = =" 2s " (1分)
B向右匀减速运动因摩擦而产生的热能为
Q1 = μmBg(υ·+ sm) (1分)
B向左匀加速运动因摩擦而产生的热能为
Q2 = μmBg(υ·- sm) (1分)
Q = Q1 + Q2 = μmBgυt = 20J (1分)
(3)设弹射装置P将A弹开时的速度为υA′,则
E = mAυA′2- mAυA2 (2分)
B离开弹簧时,AB速度互换,B的速度 υB′ = υA′ (2分)
B与弹簧分离后不再与弹簧相碰,则B滑出平台Q端,由能量关系有
mBυB′2 > μmBgL (2分)
以上三式解得
E > μmAgL- mAυA2 (2分)
代入数据解得 E> 6J (1分)
略

练习册系列答案
相关题目

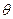 角(
角(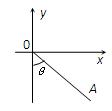
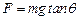 时,质点的机械能守恒
时,质点的机械能守恒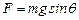 时,质点的机械能守恒
时,质点的机械能守恒