题目内容
20.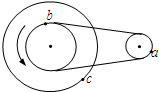 如图所示装置中,三个轮的半径分别为r、2r、4r,则图中a、b、c各点的线速度之比va:vb:vc=1:1:2;角速度之比ωa:ωb:ωc=2:1:1;周期之比Ta:Tb:Tc=1:2:2,向心加速度之比aa:ab:ac=2:1:1.
如图所示装置中,三个轮的半径分别为r、2r、4r,则图中a、b、c各点的线速度之比va:vb:vc=1:1:2;角速度之比ωa:ωb:ωc=2:1:1;周期之比Ta:Tb:Tc=1:2:2,向心加速度之比aa:ab:ac=2:1:1.
分析 a、b为共线关系,线速度相等,b、c为共轴关系,角速度相等,然后结合公式v=ωr和a=$\frac{{v}^{2}}{r}=r{ω}^{2}$两两分析.
解答 解:1、先讨论a、b两个点:
a、b为共线关系,线速度相等,故:
$\frac{{v}_{a}}{{v}_{b}}=1$
根据v=ωr,有:
$\frac{{ω}_{a}}{{ω}_{b}}=\frac{{r}_{b}}{{r}_{a}}=\frac{2}{1}$
根据a=$\frac{{v}^{2}}{r}$,有:
$\frac{{a}_{a}}{{a}_{b}}$=$\frac{{r}_{b}}{{r}_{a}}=\frac{2}{1}$
根据$T=\frac{2π}{ω}$,有:
$\frac{{T}_{a}}{{T}_{b}}=\frac{{ω}_{b}}{{ω}_{a}}=\frac{1}{2}$
2、再讨论b、c两个点:
b、c为共轴关系,角速度相等,有:
ωb=ωc
根据v=ωr,有:
$\frac{{v}_{b}}{{v}_{c}}=\frac{{r}_{b}}{{r}_{c}}=\frac{1}{2}$
根据$T=\frac{2π}{ω}$,有:
$\frac{{T}_{b}}{{T}_{c}}=\frac{{ω}_{c}}{{ω}_{b}}=\frac{2}{1}$
根据a=rω2,有:
$\frac{{a}_{b}}{{a}_{c}}=\frac{{r}_{b}}{{r}_{c}}=\frac{1}{2}$
综合有:
va:vb:vc=1:1:2
ωa:ωb:ωc=2:1:1
Ta:Tb:Tc=1:2:2
aa:ab:ac=2:1:1
故答案为:1:1:2,2:1:1,1:2:2,2:1:1.
点评 本题难度较小,注意共轴和共线关系,共轴是角速度相等,共线是线速度相等

| A. | 当离心力大于向心力时,物体将做离心运动 | |
| B. | 向心力可以改变物体运动速度的大小 | |
| C. | 做匀速圆周运动的物体的向心力是该物体所受的外力的合力 | |
| D. | 做圆周运动的物体的向心力不一定指向圆心 |
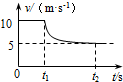 一汽车在平直公路上以20kW的功率行驶,t1时刻驶入另一段阻力恒定的平直公路,其v~t图象如图所示,已知汽车的质量为2×103kg.下列说法正确的是( )
一汽车在平直公路上以20kW的功率行驶,t1时刻驶入另一段阻力恒定的平直公路,其v~t图象如图所示,已知汽车的质量为2×103kg.下列说法正确的是( )| A. | t1前汽车受到的阻力大小为1×103N | |
| B. | t1后汽车受到的阻力大小为2×103N | |
| C. | t1时刻汽车加速度突然变为1m/s2 | |
| D. | t1~t2时间内汽车的平均速度为7.5m/s |
| A. | A物体的最大速度为$\frac{m{v}_{0}}{{m}_{A}+m}$ | |
| B. | B物体的最大速度为$\frac{m{v}_{0}}{{m}_{B}+m}$ | |
| C. | 两物体速度相同时其速度为$\frac{m{v}_{0}}{{m}_{A}+{m}_{B}+m}$ | |
| D. | 条件不足,无法计算B物体的最大速度 |
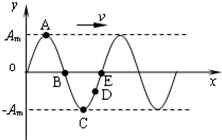
| A. | 质点A、D的振幅相等,图中所有质点都做简谐运动且振动周期相同 | |
| B. | 在该时刻质点B、E的速度大小和方向都相同 | |
| C. | 在该时刻质点A、C的加速度为零 | |
| D. | 在该时刻质点D的速度方向为+y方向 |
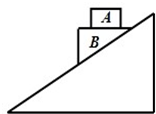 如图,光滑斜面固定于水平地面,滑块B上表面是水平的,滑块A、B保持相对静止,且一起由静止开始下滑,在斜面上运动过程中( )
如图,光滑斜面固定于水平地面,滑块B上表面是水平的,滑块A、B保持相对静止,且一起由静止开始下滑,在斜面上运动过程中( )| A. | A所受的合外力对其不做功 | B. | A只受两个力的作用 | ||
| C. | A对B不做功 | D. | B对A的弹力做正功 |
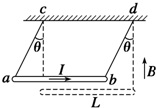 如图所示,用两根轻细悬线将质量为m、长为L的金属棒ab悬挂在c、d两处,置于竖直向上的匀强磁场内.当棒中通以从a到b的电流I后,两悬线偏离竖直方向θ角,棒处于平衡状态.则磁感应强度B为多少?为了使棒平衡在该位置上,所需磁场的最小磁感应强度B为多少?方向如何?
如图所示,用两根轻细悬线将质量为m、长为L的金属棒ab悬挂在c、d两处,置于竖直向上的匀强磁场内.当棒中通以从a到b的电流I后,两悬线偏离竖直方向θ角,棒处于平衡状态.则磁感应强度B为多少?为了使棒平衡在该位置上,所需磁场的最小磁感应强度B为多少?方向如何?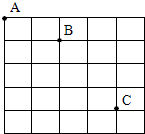 在研究平抛物体运动的实验中,用一张印有小方格的纸记录轨迹,小方格的边长L=5cm,若小球在平抛运动途中的几个位置如图中A、B、C所示,则
在研究平抛物体运动的实验中,用一张印有小方格的纸记录轨迹,小方格的边长L=5cm,若小球在平抛运动途中的几个位置如图中A、B、C所示,则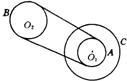 如图所示是一皮带传动装置,O1为两轮的共同轴,由O2带动.已知RB:RA=3:2,RA:RC=1:2,假若皮带不打滑,则分别在三个轮边缘的B、A、C三点角速度之比是3:2:3;线速度之比是1:1:2;向心加速度之比是3:2:6.
如图所示是一皮带传动装置,O1为两轮的共同轴,由O2带动.已知RB:RA=3:2,RA:RC=1:2,假若皮带不打滑,则分别在三个轮边缘的B、A、C三点角速度之比是3:2:3;线速度之比是1:1:2;向心加速度之比是3:2:6.