题目内容
15.一物体从O点出发,沿东偏北30°的方向运动10m至A点,然后又向正南方向运动5m至B点.(1)建立适当坐标系,描述出该物体的运动轨迹;
(2)依据建立的坐标系,分别求出A、B两点的坐标.
(3)求物体运动的位移、路程.
分析 以出发点为坐标原点,向东为x轴正方向,向北为y轴正方向,建立直角坐标系,进而描述物体的运动轨迹,求出M、N两点的坐标.
解答 解:(1)坐标系如图所示,线OAB为运动轨迹.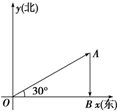
(2)xA=5$\sqrt{3}$ m,yA=5 m;xB=5$\sqrt{3}$ m,yB=0.
A点的坐标:(5$\sqrt{3}$ m,5 m),B点的坐标:(5$\sqrt{3}$ m,0).
(3)物体的位移为O到B位移为:$\sqrt{O{A}^{2}-A{B}^{2}}=\sqrt{1{0}^{2}-{5}^{2}}=5\sqrt{3}$m,方向向东
路程为10m+5m=15m.
答:(1)建立适当坐标系,描述出该物体的运动轨迹如图;
(2)依据建立的坐标系,A点的坐标:(5$\sqrt{3}$ m,5 m),B点的坐标:(5$\sqrt{3}$ m,0).
(3)位移为5$\sqrt{3}$m,方向向东,路程为15m.
点评 本题的关键是根据几何关系确定B点的位置,要求同学们能正确建立合适的坐标系,难度不大,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6. 如图所示,质量为m的小滑块放在半径为R、质量为M的半球体上,两物体都静止不动,半球体与水平地、小滑块与半球体间的动摩擦因数均为μ,质点与球心的连线与水平地面的夹角为θ,则下列说法正确的是( )
如图所示,质量为m的小滑块放在半径为R、质量为M的半球体上,两物体都静止不动,半球体与水平地、小滑块与半球体间的动摩擦因数均为μ,质点与球心的连线与水平地面的夹角为θ,则下列说法正确的是( )
 如图所示,质量为m的小滑块放在半径为R、质量为M的半球体上,两物体都静止不动,半球体与水平地、小滑块与半球体间的动摩擦因数均为μ,质点与球心的连线与水平地面的夹角为θ,则下列说法正确的是( )
如图所示,质量为m的小滑块放在半径为R、质量为M的半球体上,两物体都静止不动,半球体与水平地、小滑块与半球体间的动摩擦因数均为μ,质点与球心的连线与水平地面的夹角为θ,则下列说法正确的是( )| A. | 地面对半球体的摩擦力方向水平向左 | |
| B. | 小滑块对半球体的压力大小为mgcosθ | |
| C. | 小滑块所受摩擦力大小为μmgsinθ | |
| D. | 半球体对地面的压力等于(M+m)g |
3. 如图在固定斜面上的一物块受到一外力F的作用,F平行单于斜面向上.若要物块在斜面上保持静止,F的取值应有一定范围,已知其最大值和最小值分别为F1和F2(F2>0).由此不可求出( )
如图在固定斜面上的一物块受到一外力F的作用,F平行单于斜面向上.若要物块在斜面上保持静止,F的取值应有一定范围,已知其最大值和最小值分别为F1和F2(F2>0).由此不可求出( )
 如图在固定斜面上的一物块受到一外力F的作用,F平行单于斜面向上.若要物块在斜面上保持静止,F的取值应有一定范围,已知其最大值和最小值分别为F1和F2(F2>0).由此不可求出( )
如图在固定斜面上的一物块受到一外力F的作用,F平行单于斜面向上.若要物块在斜面上保持静止,F的取值应有一定范围,已知其最大值和最小值分别为F1和F2(F2>0).由此不可求出( )| A. | 物块的质量 | B. | 斜面的倾角 | ||
| C. | 物块与斜面间的最大静摩擦力 | D. | 物块对斜面的正压力 |
10.关于抛体运动的下列说法中正确的是( )
| A. | 抛体运动一定是曲线运动 | B. | 抛体运动一定是直线运动 | ||
| C. | 抛体运动一定是匀变速运动 | D. | 抛体运动一定是加速度变化的运动 |
20.如图所示,要使灯泡变得更亮,下列措施可行的是( )


| A. | 其他条件不变,仅减小R的长度 | |
| B. | 其他条件不变,仅增大R的横截面积 | |
| C. | 保持R形状、尺寸不变,改用电阻率更大的材料 | |
| D. | 保持R形状、尺寸不变,改用电阻率更小的材料 |
4.两木块A、B质量之比为2:1,在水平地面上滑行时与地面间的动摩擦因数相同,则A、B在开始滑行到停止运动的过程中,滑行的时间之比和距离之比( )
| A. | 初动能相同时分别为1:$\sqrt{2}$和1:2 | B. | 初动能相同时分别为1:2和1:4 | ||
| C. | 初动量相同时分别为1:$\sqrt{2}$和1:2 | D. | 初动量相同时分别为1:2和1:4 |
19. 某同学要探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k.做法是先将待测弹簧的一端固定在铁架台上.然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上,当弹簧自然下垂时,指针指示的刻度值记作l0,弹簧下端每增加一个50g的砝码时,指针示数分别记作l1、l2、…l5,g取9.8m/s2.
某同学要探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k.做法是先将待测弹簧的一端固定在铁架台上.然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上,当弹簧自然下垂时,指针指示的刻度值记作l0,弹簧下端每增加一个50g的砝码时,指针示数分别记作l1、l2、…l5,g取9.8m/s2.
(1)下表记录的是该同学测出的5个值,其中l0未记录.
以砝码的数目n为纵轴,以弹簧的长度l为横轴,根据表格中的数据,在如下坐标纸中作出n-l图线.
(2)根据n-l图线,可知弹簧的劲度系数k=28N/m.(保留2位有效数字)
(3)根据n-l图线,可知弹簧的原长l0=1.70cm.
 某同学要探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k.做法是先将待测弹簧的一端固定在铁架台上.然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上,当弹簧自然下垂时,指针指示的刻度值记作l0,弹簧下端每增加一个50g的砝码时,指针示数分别记作l1、l2、…l5,g取9.8m/s2.
某同学要探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k.做法是先将待测弹簧的一端固定在铁架台上.然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上,当弹簧自然下垂时,指针指示的刻度值记作l0,弹簧下端每增加一个50g的砝码时,指针示数分别记作l1、l2、…l5,g取9.8m/s2.(1)下表记录的是该同学测出的5个值,其中l0未记录.
| 代表符号 | l0 | l1 | l2 | l3 | l4 | l5 |
| 刻度值/cm | 3.40 | 5.10 | 6.85 | 8.60 | 10.30 |
(2)根据n-l图线,可知弹簧的劲度系数k=28N/m.(保留2位有效数字)
(3)根据n-l图线,可知弹簧的原长l0=1.70cm.
