题目内容
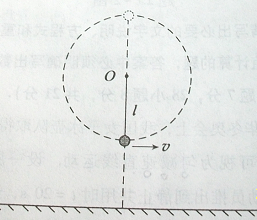
如图所示，ABC是光滑轨道，其中BC部分是半径为R的竖直放置的半圆．一质量为M的小木块放在轨道水平部分，木块被水平飞来的质量为m的子弹射中，并滞留在木块中．若被击中的木块沿轨道能滑到最高点C，已知木块对C点的压力大小为(M+m)g，求：子弹射入木块前瞬间速度的大小．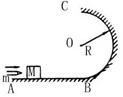
试题分析：设子弹射入木块瞬间速度为v，射入木块后的速度为vB，到达C点
时的速度为vC。
子弹射入木块时，系统动量守恒，可得：
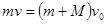① （3分）木块(含子弹)在BC段运动，满足机械能守恒条件，可得
② （4分）木块(含子弹)在C点做圆周运动，设轨道对木块的弹力为T，
木块对轨道的压力为T′，可得：
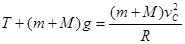③ （4分）又：T =T′=(M+m)g ④
由①、②、③、④方程联立解得：
子弹射入木块前瞬间的速度：
（2分）点评：对于圆周运动，常常是机械能守恒定律或动能定理与牛顿定律的综合．子弹射击木块过程，基本的规律是动量守恒．
练习册系列答案
相关题目
平抛，小球碰到轨道后不反弹（沿轨道径向速度减为0），忽略一切阻力，求：
