��Ŀ����
����Ŀ����ͼ��ʾ����ֽ���ڽ���ֱ������ϵxOy���Եڢ������ڵ�ֱ��OM���븺x���45���������y��Ϊ�磬��x��0����������ǿ�糡������ˮƽ����ǿ��СE=0��32V/m����ֱ��OM����x��Ϊ�磬��y��0����������ֱֽ���������ǿ�ų����Ÿ�Ӧǿ��B=0��1T��һ���������Ĵ��������ӣ�������ԭ��O��y�Ḻ������v0=2��103m/s�ij��ٶ�����ų�����֪���ӵıȺ�Ϊq/m=5��106C/kg����
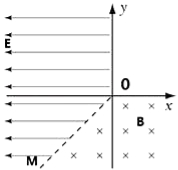
��1�����ӵ�һ�ξ����ų��߽�ʱ��λ������
��2�������ڴų������˶�����ʱ��
��3�����������뿪��ų�����ʱ��λ��������
���𰸡���1������4��10��3m����4��10��3m������2��1��265��10��5s����3����0��0��192m����
��������
�����������1�����Ӵ����磬��O����y�Ḻ��������ų�����˳ʱ�뷽����Բ���˶���
��һ�ξ����ų��߽��ϵ�һ������ΪA��������![]() �ã�
�ã�![]() ��
��
���ԣ�A�������Ϊ������4��10��3m����4��10��3m��
��2���������ڴų�����Բ���˶�������ΪT���ڶ��γ��ų��ĵ�ΪC���ڶ��ν���ų����˶�Ϊ![]() Բ�ܣ������ڴų����˶�����ʱ��Ϊ��
Բ�ܣ������ڴų����˶�����ʱ��Ϊ��![]() ��
�� ![]()
�������ݽ�ã�T=1��265��10��5s������t=1��265��10��5s
��3�����Ӵ�C����y�����������糡������ƽ���˶�����![]() ��
��
��ƽ���ɵã�![]() ��y=v0t1
��y=v0t1
�������ݽ�ã���y=0��2m y=��y��2r=0��2m��2��4��10��3m=0��192m
�����뿪��ų�ʱ��λ������Ϊ����0��0��192m����

 ��һ������ĩ�ٷֳ�̾�ϵ�д�
��һ������ĩ�ٷֳ�̾�ϵ�д�