题目内容
如图所示，质量不计的光滑直杆AB的A端固定一个小球P，杆OB段套着小球Q，Q与轻质弹簧的一端相连,弹簧的另一端固定在O点，弹簧原长为L，劲度系数为k，两球的质量均为m,OA=d，小球半径忽略.现使在竖直平面内绕过O点的水平轴转动，若OB段足够长，弹簧形变始终处于弹性限度内。当球P转至最高点时，球P对杆的作用力为零，求此时弹簧的弹力。
解析:：设P到最高点时,角速度为w;此时弹簧弹力为F,弹簧长度为L′.
则对P：mg=mw2d;
对Q：F-mg=mw2L′
又F=k(L′-L)
联立可得 F=
练习册系列答案
相关题目
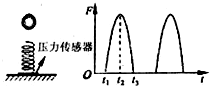如图所示，质量不计的活塞把一定质量的理想气体封闭在上端开口的直立圆筒形气缸中，活塞上堆放细沙，活塞处于静止状态．现在对气体缓慢加热，同时不断去走细沙，使活塞缓慢上升，直到细沙全部取走，则在此过程中（ ）
（2010?崇明县一模）如图所示，质量不计的光滑活塞被销钉固定，使一定量气体被封闭在容器的上部，容器下部与大气连通，容器上部连接有一U形管（U形管内气体的体积忽略不计，容器下部足够高）．此时容器上部封闭气体的体积为V，室温为T1=300K，U形管两
如图所示，质量不计的定滑轮以轻绳牵挂在 B点，另一条轻绳一端系重物G，绕过滑轮后，另一端固定在墙上A点．若改变 B点位置使滑轮位置发生移动，但使AO段绳子始终保持水平，则可以判断悬点B所受拉力T的大小变化情况是（ ）
如图所示，质量不计的定滑轮通过轻绳挂在B点，轻绳的一端系一重物G，绕过滑轮后另一端固定在墙上的A点，使整个装置处于平衡状态．现将B点向左或向右缓慢移动一点，若移动前后AO仍处于水平，并且装置处于平衡状态，不计摩擦，则悬点B受绳的拉力F和与水平方向的夹角θ的情况是（ ）
如图所示，质量不计的弹簧竖直固定在水平面上，t=0时刻，将一金属小球从弹簧正上方某一高度处由静止释放，小球接触弹簧并将弹簧压缩至最低点（形变在弹性限度内），然后又被弹起离开弹簧，上升到一定高度后又下落，如此反复．通过安装在弹簧下端的压力传感器，测出该过程中弹簧弹力F随时间t变化的图象如图所示，则（ ）| A、运动过程中小球的机械能守恒 | B、t2时刻小球的加速度为零 | C、t1～t2这段时间内，小球的动能与重力势能之和在减小 | D、t2～t3这段时间内，小球的动能在逐渐增加 |