题目内容
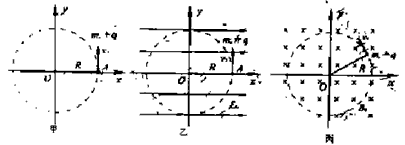
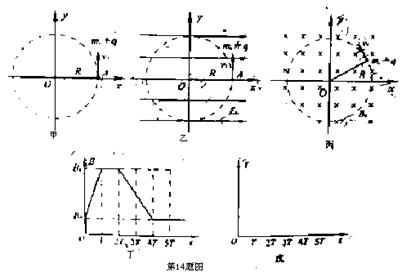
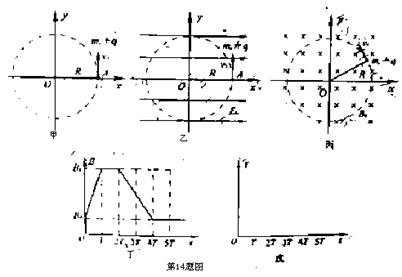
不可伸长的绝缘轻绳长为R,一端系于O点,另一端系一质量为m、电量为+q 的点电荷,点电荷可在xoy平面内绕O点做半径为R的圆周运动,如图甲所示,本题计算中忽略点电荷的重力.
(1)当点电荷以速率v0沿+y方向通过A(R,0)点的瞬间,在空间中加沿x轴正方向的匀强电场E0,如图乙所示,要使点电荷能做完整的圆周运动,电场强度E0需满足何条件?
(2)在(1)问中,其他条件不变,将空间中的电场用垂直xoy平面向里的匀强磁场B0代替,如图所示,要使点电荷仍能做半径为R的圆周运动,磁感应强度B0需满足何条件?
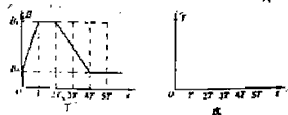
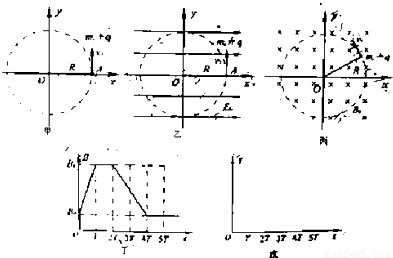
(3)变化的磁场周围可以激发感生电场,若上述磁场随时间均匀变化,会在点电荷运动的圆形轨道上产生一个环形电场,其电场线是闭合的,各点场强大小相等.现在空间加一垂直xoy平面向里的匀强磁场,其磁感应强度B变化情况如图丁所示,t=0时刻点电荷的速率为v0,轻绳一直处于伸直状态.试求0~T时间内,轨道中形成的感生电场E感的大小,并在图戊中作出点电荷在0~5T时间内v~t图象,要求写出主要的分析过程.
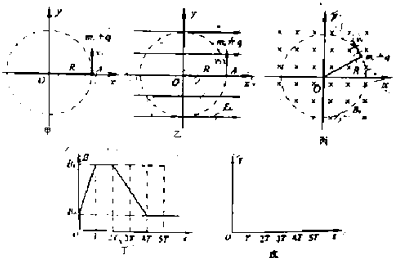
(1)当点电荷以速率v0沿+y方向通过A(R,0)点的瞬间,在空间中加沿x轴正方向的匀强电场E0,如图乙所示,要使点电荷能做完整的圆周运动,电场强度E0需满足何条件?
(2)在(1)问中,其他条件不变,将空间中的电场用垂直xoy平面向里的匀强磁场B0代替,如图所示,要使点电荷仍能做半径为R的圆周运动,磁感应强度B0需满足何条件?
(3)变化的磁场周围可以激发感生电场,若上述磁场随时间均匀变化,会在点电荷运动的圆形轨道上产生一个环形电场,其电场线是闭合的,各点场强大小相等.现在空间加一垂直xoy平面向里的匀强磁场,其磁感应强度B变化情况如图丁所示,t=0时刻点电荷的速率为v0,轻绳一直处于伸直状态.试求0~T时间内,轨道中形成的感生电场E感的大小,并在图戊中作出点电荷在0~5T时间内v~t图象,要求写出主要的分析过程.

分析:(1)要使点电荷能做完整的圆周运动,当点电荷运动到最左端绳子张力F≥0.先根据动能定理求出此时电荷的速度,由牛顿第二定律和向心力公式结合求E0需满足的条件.
(2)磁场垂直纸面向内,对点电荷产生的洛伦兹力始终指向O点,由洛伦兹力与绳子拉力的合力提供向心力时,点电荷能做完整的圆周运动,绳子的拉力F′≥0,由牛顿第二定律列式求解.
(3)分四段时间分析,根据法拉第电磁感应定律求感生电动势,当感生电动势一定时,点电荷所受电场力大小一定,在圆形轨道上作匀加速圆周运动,由牛顿第二定律求出速度的表达式;当感生电动势为零时,点电荷不所受电场力,在圆形轨道上作匀速圆周运动.
(2)磁场垂直纸面向内,对点电荷产生的洛伦兹力始终指向O点,由洛伦兹力与绳子拉力的合力提供向心力时,点电荷能做完整的圆周运动,绳子的拉力F′≥0,由牛顿第二定律列式求解.
(3)分四段时间分析,根据法拉第电磁感应定律求感生电动势,当感生电动势一定时,点电荷所受电场力大小一定,在圆形轨道上作匀加速圆周运动,由牛顿第二定律求出速度的表达式;当感生电动势为零时,点电荷不所受电场力,在圆形轨道上作匀速圆周运动.
解答:解:(1)分析可知,点电荷运动到最左端绳子张力最小,设此时速度大小为v
由动能定理-qE0-2R=
mv2-
m
在最左端时qE0+F=m
得F=
当F≥0时,点电荷能做完整圆周运动,解得E0≤
(2)磁场垂直纸面向内,对点电荷产生的洛伦兹力始终指向O点,
对任一点进行受力分析有qv0B+F′=
得F′=
-qvoB
当F′≥0时,点电荷能做完整的圆周运动,解得B0≤
(3)0至T时间内磁场均匀变化,激发的感生电动势为E,则
E=
=S
=πR2
感生电场的场强 E感=
=
①0~T时间内,磁场均匀增加,感生电场的场强大小一定,点电荷在圆形轨道上作匀加速圆周运动,加速度大小a=
=
经时间T后,速度大小v1=v0+aT=v0+
②T~2T时间内磁场不变,感生电场的场强为零,点电荷在圆形轨道上作匀速圆周运动,速率v1不变.
③2T~4T时间内磁场均匀减小,感生电场的场强大小一定,点电荷在圆形轨道上作匀
减速圆周运动,加速度大小a′=
=
=
经时间2T后,v2=v1-a′(2T)=v0+
-
=v0
④4T~5T时间内磁场变,感生电场的场强为零,点电荷在圆形轨道上作匀速圆周运动,速率v0不变.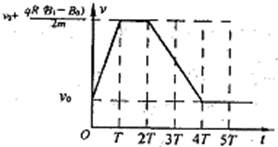
根据以上结果,作图如下.
答:
(1)电场强度E0需满足E0≤
.
(2)磁感应强度B0需满足得B0≤
.
(3)0~T时间内,轨道中形成的感生电场E感的大小为
.点电荷在0~5T时间内v~t图象如图所示.
由动能定理-qE0-2R=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
在最左端时qE0+F=m
| v2 |
| R |
得F=
m
| ||
| R |
当F≥0时,点电荷能做完整圆周运动,解得E0≤
m
| ||
| 5qR |
(2)磁场垂直纸面向内,对点电荷产生的洛伦兹力始终指向O点,
对任一点进行受力分析有qv0B+F′=
m
| ||
| R |
得F′=
m
| ||
| R |
当F′≥0时,点电荷能做完整的圆周运动,解得B0≤
| mv0 |
| qR |
(3)0至T时间内磁场均匀变化,激发的感生电动势为E,则
E=
| △φ |
| △t |
| △B |
| △t |
| (B1-B0) |
| T |
感生电场的场强 E感=
| E |
| 2πR |
| R(B1-B0) |
| 2T |
①0~T时间内,磁场均匀增加,感生电场的场强大小一定,点电荷在圆形轨道上作匀加速圆周运动,加速度大小a=
| qE感 |
| m |
| qR(B1-B0) |
| 2mT |
经时间T后,速度大小v1=v0+aT=v0+
| qR(B1-B0) |
| 2m |
②T~2T时间内磁场不变,感生电场的场强为零,点电荷在圆形轨道上作匀速圆周运动,速率v1不变.
③2T~4T时间内磁场均匀减小,感生电场的场强大小一定,点电荷在圆形轨道上作匀
减速圆周运动,加速度大小a′=
| qE感 |
| m |
| qR(B1-B0) |
| 4mT |
| a |
| 2 |
经时间2T后,v2=v1-a′(2T)=v0+
| qR(B1-B0) |
| 4mT |
| qR(B1-B0) |
| 2m |
④4T~5T时间内磁场变,感生电场的场强为零,点电荷在圆形轨道上作匀速圆周运动,速率v0不变.

根据以上结果,作图如下.
答:
(1)电场强度E0需满足E0≤
m
| ||
| 5qR |
(2)磁感应强度B0需满足得B0≤
| mv0 |
| qR |
(3)0~T时间内,轨道中形成的感生电场E感的大小为
| R(B1-B0) |
| 2T |
点评:本题中带电粒子在复合场中做圆周运动时,关键要找出物理的“最高点”,分析临界条件,只要点电荷能通过此点,就能做完整的圆周运动,可与重力场中竖直平面内的圆周运动类比,运用动能定理和牛顿第二定律进行分析求解.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
不可伸长的绝缘轻绳长为![]() ,一端系于O点,另一端系一质量为
,一端系于O点,另一端系一质量为![]() 、电量为
、电量为![]() 的点电荷,点电荷可在
的点电荷,点电荷可在![]() 平面内绕O点做半径为
平面内绕O点做半径为![]() 的圆周运动,如图甲所示,本题计算中忽略点电荷的重力。
的圆周运动,如图甲所示,本题计算中忽略点电荷的重力。
(1)当点电荷以速率![]() 沿
沿![]() 方向通过A(R,0)点的瞬间,在空间中加沿
方向通过A(R,0)点的瞬间,在空间中加沿![]() 轴正方向的匀强电场
轴正方向的匀强电场![]() ,如图乙所示,要使点电荷能做完整的圆周运动,电场强度
,如图乙所示,要使点电荷能做完整的圆周运动,电场强度![]() 需满足何条件?
需满足何条件?
(2)在(1)问中,其他条件不变,将空间中的电场用垂直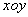 平面向里的匀强磁场
平面向里的匀强磁场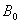 代替,如图所示,要使点电荷仍能做半径为
代替,如图所示,要使点电荷仍能做半径为![]() 的圆周运动,磁感应强度
的圆周运动,磁感应强度![]() 需满足何条件?
需满足何条件?
|
不可伸长的绝缘轻绳长为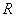 ,一端系于O点,另一端系一质量为
,一端系于O点,另一端系一质量为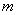 、电量为
、电量为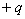 的点电荷,点电荷可在
的点电荷,点电荷可在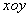 平面内绕O点做半径为
平面内绕O点做半径为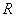 的圆周运动,如图甲所示,本题计算中忽略点电荷的重力。
的圆周运动,如图甲所示,本题计算中忽略点电荷的重力。
(1)当点电荷以速率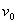 沿
沿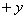 方向通过A(R,0)点的瞬间,在空间中加沿
方向通过A(R,0)点的瞬间,在空间中加沿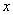 轴正方向的匀强电场
轴正方向的匀强电场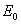 ,如图乙所示,要使点电荷能做完整的圆周运动,电场强度
,如图乙所示,要使点电荷能做完整的圆周运动,电场强度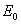 需满足何条件?
需满足何条件?
(2)在(1)问中,其他条件不变,将空间中的电场用垂直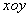 平面向里的匀强磁场
平面向里的匀强磁场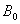 代替,如图所示,要使点电荷仍能做半径为
代替,如图所示,要使点电荷仍能做半径为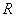 的圆周运动,磁感应强度
的圆周运动,磁感应强度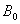 需满足何条件?
需满足何条件?
|
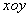 平面向里的匀强磁场,其磁感应强度B变化情况如图丁所示,
平面向里的匀强磁场,其磁感应强度B变化情况如图丁所示,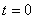 时刻点电荷的速率为
时刻点电荷的速率为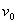 ,轻绳一直处于伸直状态。试求
,轻绳一直处于伸直状态。试求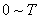 时间内,轨道中形成的感生电场
时间内,轨道中形成的感生电场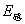 的大小,并在图戊中作出点电荷在
的大小,并在图戊中作出点电荷在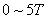 时间内
时间内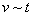 图像,要求写出主要的分析过程。
图像,要求写出主要的分析过程。
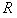 ,一端系于O点,另一端系一质量为
,一端系于O点,另一端系一质量为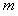 、电量为
、电量为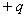 的点电荷,点电荷可在
的点电荷,点电荷可在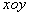 平面内绕O点做半径为
平面内绕O点做半径为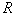 的圆周运动,如图甲所示,本题计算中忽略点电荷的重力。
的圆周运动,如图甲所示,本题计算中忽略点电荷的重力。 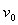 沿
沿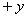 方向通过A(R,0)点的瞬间,在空间中加沿
方向通过A(R,0)点的瞬间,在空间中加沿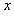 轴正方向的匀强电场
轴正方向的匀强电场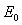 ,如图乙所示,要使点电荷能做完整的圆周运动,电场强度需满足何条件?
,如图乙所示,要使点电荷能做完整的圆周运动,电场强度需满足何条件? 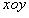 平面向里的匀强磁场
平面向里的匀强磁场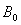 代替,如图所示,要使点电荷仍能做半径为
代替,如图所示,要使点电荷仍能做半径为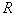 的圆周运动,磁感应强度
的圆周运动,磁感应强度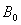 需满足何条件?
需满足何条件?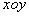 平面向里的匀强磁场,其磁感应强度B变化情况如图丁所示,
平面向里的匀强磁场,其磁感应强度B变化情况如图丁所示,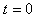 时刻点电荷的速率为
时刻点电荷的速率为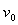 ,轻绳一直处于伸直状态。试求
,轻绳一直处于伸直状态。试求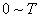 时间内,轨道中形成的感生电场
时间内,轨道中形成的感生电场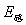 的大小,并在图戊中作出点电荷在时间
的大小,并在图戊中作出点电荷在时间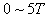 内
内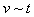 图像,要求写出主要的分析过程。
图像,要求写出主要的分析过程。