题目内容
7. 一个圆柱形的竖直的井里存有一定量的水,井的侧面和底部是密闭和.在井中固定地插着一根两端开口的薄壁圆管,管和井共轴,管下端未触及井底,在圆管内有一不漏气的活塞,它可沿圆管上下滑动.开始时,管内外水面相齐,且活塞恰好接触水面,如图所示,现有卷扬机通过绳子对活塞施加一个向上的力F,使活塞缓慢向上移动.已知管筒半径r=0.100m,井的半径R=2r,水的密度ρ=1.00×103kg/m3,大气压p0=1.00×105Pa.,(井和管在水面以上及水面以下的部分都足够长.不计活塞质量,不计摩擦,重力加速度g=10m/s2.)求:
一个圆柱形的竖直的井里存有一定量的水,井的侧面和底部是密闭和.在井中固定地插着一根两端开口的薄壁圆管,管和井共轴,管下端未触及井底,在圆管内有一不漏气的活塞,它可沿圆管上下滑动.开始时,管内外水面相齐,且活塞恰好接触水面,如图所示,现有卷扬机通过绳子对活塞施加一个向上的力F,使活塞缓慢向上移动.已知管筒半径r=0.100m,井的半径R=2r,水的密度ρ=1.00×103kg/m3,大气压p0=1.00×105Pa.,(井和管在水面以上及水面以下的部分都足够长.不计活塞质量,不计摩擦,重力加速度g=10m/s2.)求:(1)管内水面上升的高度h1与管外水面下降的高度h2之比
(2)活寒上升H=9.00m的过程中拉力F所做的功.
分析 解决本题需要掌握:液体压强的产生;正确判断活塞和液面之间是否出现真空;活塞上升过程分为两个过程,正确求出这两个过程中拉力做功;在求功过程中,对于变力做功,要正确应用功能关系求解.
解答 解:从开始提升到活塞升至内外水面高度差为${h_0}=\frac{p_0}{ρg}=10m$的过程中,活塞始终与管内液体接触,设活塞上升距离为h1,管外液面下降距离为h2,
h0=h1+h2…①
因液体体积不变,有:${h_2}={h_1}(\frac{{π{r^2}}}{{π{R^2}-πr}})=\frac{1}{3}{h_1}$…②
得:${h_1}=\frac{3}{4}{h_0}=\frac{3}{4}×10m=7.5m$…③
题给H=9m>h1,由此可知确实有活塞下面是真空的一段过程.
活塞移动距离从零到h1的过程中,对于水和活塞这个整体,其机械能的增量应等于除重力外其他力所做的功,因为始终无动能,所以机 械能的增量也就等于重力势能增量,即:
械能的增量也就等于重力势能增量,即:
$△E=ρ(π{r^2}{h_1})g\frac{h_0}{2}$…④
其他力有管内、外的大气压力的拉力F,因为液体不可压缩,所以管内、外大气压力做的总功${p_0}π({R^2}-{r^2}){h_2}-{p_0}πr{h_1}=0$,故外力做功就只是拉力F做的功,由功能关系知W1=△E…⑤
即 ${W_1}=ρ(π{r^2})g\frac{3}{8}h_0^2=\frac{3}{8}π{r^2}\frac{p_0^2}{ρg}=1.18×{10^4}J$…⑥
活塞移动距离从h1到H的过程中,液面不变,F是恒力F=πr2p0,做功为:${W_2}=F(H-{h_1})=π{r^2}{p_0}(H-{h_1})=4.71×{10^3}J$…⑦
所求拉力F做的总功为:${W_1}+{W_2}=1.65×{10^4}J$…⑧
答:(1)管内水面上升的高度h1与管外水面下降的高度h2之比3:1.
(2)活寒上升H=9.00m的过程中拉力F所做的功为1.65×104J.
点评 本题涉及有关压强的运算,又涉及功能关系,而且过程比较复杂,尤其是要判断活塞和液面之间是否出现真空.无论多么复杂过程,都是由一些简单无论过程组成,要注重过程分析,正确选用所学规律进行求解.本题难度较大.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案| A. | 长度 | B. | 质量 | C. | 时间 | D. | 加速度 |
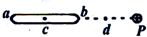
| A. | a端的电势比b端的高 | B. | a端的电势比b点的低 | ||
| C. | a端的电势比d点的低 | D. | c处场强不为零 |
 如图所示为一物体做直线运动时的图象,但纵坐标表示的物理量未标出.已知物体在前2s内向东运动,则以下判断正确的是( )
如图所示为一物体做直线运动时的图象,但纵坐标表示的物理量未标出.已知物体在前2s内向东运动,则以下判断正确的是( )| A. | 若纵坐标表示位移,则物体在4s内的位移为零 | |
| B. | 若纵坐标表示位移,则物体在4s内的运动方向始终向东 | |
| C. | 若纵坐标表示速度,则物体在4s内的平均速度为零 | |
| D. | 若纵坐标表示速度,则物体在4s内的加速度大小不变,加速度的方向先向东再向西 |
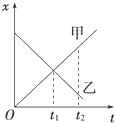
| A. | 甲物体做匀加速直线运动,乙物体做匀减速直线运动 | |
| B. | 甲、乙两物体在t1时刻相遇 | |
| C. | 甲、乙两物体运动的方向相反 | |
| D. | 在t1时刻之后甲的速度总是大于乙的速度 |
 一只矩形线圈在匀强磁场中绕垂直于磁感线的轴匀速转动,穿过线圈的磁通量随时间变化的图象如图所示,则下列说法中正确的是( )
一只矩形线圈在匀强磁场中绕垂直于磁感线的轴匀速转动,穿过线圈的磁通量随时间变化的图象如图所示,则下列说法中正确的是( )| A. | t=0时刻,线圈平面处于中性面 | |
| B. | t=0.01s时刻,磁通量的变化率最大 | |
| C. | t=0.02s时刻,交流电动势达到最大 | |
| D. | t=0.02s时刻,线圈的磁通量达到最大 |
| A. | 匀速圆周运动就是匀速运动 | B. | 匀速圆周运动是变速运动 | ||
| C. | 角速度越大,周期一定越小 | D. | 线速度越大,周期一定越小 |
 一列横波沿x轴正方向传播,在t=0时刻的波形曲线如图所示.已知这列波的质点P连续出现两次波峰的时间间隔为0.4s,则( )
一列横波沿x轴正方向传播,在t=0时刻的波形曲线如图所示.已知这列波的质点P连续出现两次波峰的时间间隔为0.4s,则( )| A. | 这列波的波长为5 m | |
| B. | 这列波的传播速度为10 m/s | |
| C. | 当t=0.7 s时,质点Q第一次到达波峰 | |
| D. | 质点Q到达波峰时,质点P恰好到达波谷 |
 如图所示,当平行板电容器充电后,静电计的指针偏转一定角度.若不改变A、B两极板的带电荷量而减小两极板间的距离,同时在两极板间插入电介质,则静电计指针的偏转角度将减小.
如图所示,当平行板电容器充电后,静电计的指针偏转一定角度.若不改变A、B两极板的带电荷量而减小两极板间的距离,同时在两极板间插入电介质,则静电计指针的偏转角度将减小.