题目内容
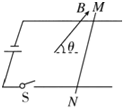
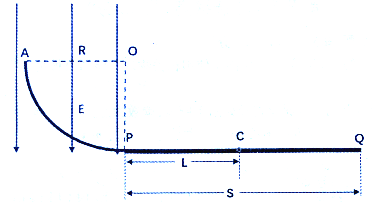
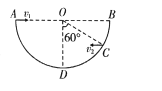
【题目】如图所示，水平地面上有一个半球形大坑，O为球心，AB为沿水平方向的直径。若在A 点以初速度v1沿AB方向向右平抛一小球甲，小球甲将击中坑内的最低点D;若在甲球抛出的同时，在C点以初速度v2沿平行BA方向向左平抛另一小球乙，也恰能击中D点。已知∠COD=60°，甲、乙两小球的质量相同，不计空气阻力，则
A. 甲、乙两小球初速度的大小之比v1：v2= 
：3
B. 在击中D点前的瞬间，重力对甲、乙两小球做功的瞬时功率之比为
：1
C. 甲、乙两球在此过程中速度变化量的大小之比为2:1
D. 逐渐增大小球甲抛出速度v1的大小，甲球可能垂直撞到坑内BCD上
【答案】AB
【解析】根据几何关系知，下降的高度之比2：1，根据： 
，可得时间之比为： 
，根据： 
，因为水平位移之比为
，解得两小球初速度之比
，故A正确；根据
，以及P=mgvy知，重力做功的瞬时功率
，根据几何关系知，下降的高度之比2：1，则重力做功的瞬时功率之比
，故B正确；平抛小球速度的变化量即为竖直分速度，而竖直分速度与下落的时间成正比，所以两球速度变化量的大小之比应为
，故C错误；逐渐增大小球甲抛出时速度的大小甲球不可能垂直撞到球壁BCD上，因为根据平抛速度的反向延长线过水平位移的中点这一推论，垂直撞到球壁的速度反向延长线必定过圆心O，而O点不是水平位移的中点，故D错误。所以AB正确，CD错误。
练习册系列答案
阅读快车系列答案
相关题目
