题目内容

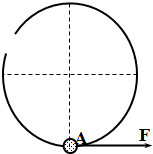如图所示，质量为4千克的小圆环穿在半径为0.5m的光滑圆形竖直轨道上，现用大小为30N、方向始终保持水平向右的力F作用在位于圆形轨道最低点A处的小圆环上，小圆环从静止开始沿轨道向上运动．则小圆环在向上运动过程中达到的最大动能为
5
5
J，小圆环到达的最高点与最低点A的高度差为
0.36
0.36
m．（g取10m/s2）
分析：由于小圆环恰好经过圆环形轨道上等效最低点时，重力和F的合力沿半径离开圆心时，圆环的动能最大．根据力的合成确定等效最低点的位置，再运用动能定理得出最大动能；
当圆环的速度为零时，到达最高点，根据动能定理求解最高点与最低点A的高度差．
解答：解：设圆环运动到B点时，重力和F的合力沿半径离开圆心，B点为等效的最低点，此位置小圆环的动能最大．设B与圆心连线与竖直方向的夹角为α
则 tanα=
F
mg
=
3
4
，则得sinα=
3
5
，cosα=
4
5

圆环从A到B的过程，由动能定理得：Ek=-mgR（1-cosα）+FRsinα
代入解得，最大动能为Ek=5J
当圆环的速度为零时，到达最高点，设最高点与圆心连线与竖直方向的夹角为θ
根据动能定理得：FRsinθ-mgR（1-cosθ）=0
最高点与最低点A的高度差为h=R（1-cosθ）
联立解得h=0.36m
故答案为：5，0.36
点评：本题是动能定理和临界条件的综合应用，可采用类比的方法，将圆环的运动与单摆运动比较，找到等效最低点．
练习册系列答案
相关题目
（1）如图所示为某同学“探究弹簧弹力跟伸长的关系”的实验装置图，所用钩码的重力相当于对弹簧提供了向右的恒定的拉力．
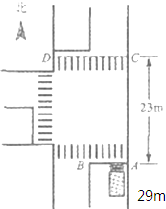精英家教网
（Ⅰ）实验的步骤如下：
①把细绳和弹簧的小环结好，让细绳跨过定滑轮，并结好细绳套．
②从刻度尺上读出弹簧左侧结点到小环结点的距离（即原长）．
③在细绳套上挂上1个已知质量的钩码，待
 
到稳定时，从刻度尺上读出弹簧的长度，再计算此时的伸长量，和钩码的质量一并填入列表．
④换上2个、3个、4个、5个钩码挂上细绳套；重复③的步骤，得到五组数据．
⑤以弹力（钩码质量换算过来）为纵坐标，以
 
为横坐标，根据所测数据在坐标纸上描点，作出一条平滑的直线，归纳出实验的结论．
（Ⅱ）如图是弹簧弹力F与弹簧伸长量x的F-x图线，由此可弹得到结论：弹力F与弹簧伸长量x为
 
关系．图线不过原点的原因是由于
 
．
（2）在测定一节干电池的电动势和内电阻的实验中，实物摆放的位置如图所示．
①请用笔画线代替导线将实物图中未完成的3条连接线连接好．
②根据所连的图说明在开关S闭合之前，滑动变阻器的触头P应放
 
端．
③如果把干电池换成内阻约几千欧姆的水果电池，按上面连接的电路进行实验测量，则电压表的
 
引起的误差将大大增加，这时必须把电压表改为并联在
 
上才能减小误差．
（1）用多用电表测量阻值约十几千欧的电阻Rx．S为电表的选择开关，P为欧姆挡调零旋钮．
①从以下给出的操作步骤中，选择必要的步骤，并排出合理顺序：
 
．
（填步骤前的字母）
A．旋转s至欧姆挡“×lk”
B．旋转s至欧姆挡“×100”
C．旋转S至“OFF”，并拔出两表笔
D．将两表笔分别连接到Rx，的两端，
读出阻值后，断开两表笔
E．将两表笔短接，调节P使指针对准刻度盘上欧姆挡的零刻度，断开两表笔
②按正确步骤测量时，指针指在图1示位置，Rx的测量值为
 
 kΩ．精英家教网
（2）某实验小组在“探究加速度与物体受力的关系”实验中，设计出如下的实验方案，其实验装置如图所示．已知小车质量
M=214.6g，砝码盘质量mo=7.5g，所使用的打点计时器交流电频率f=50Hz．其实验步骤是：
 

A．按图2中所示安装好实验装置；
B．调节长木板的倾角，轻推小车后，
使小车能沿长木板向下做匀速运动；
C．取下细绳和砝码盘，记下砝码盘中砝码的质量m；
D．先接通电源，再放开小车，打出一条纸带，由纸带求得小车的加速度a；
E．重新挂上细绳和砝码盘，改变砝码盘中砝码质量，重复B-D步骤，求得小车在不同合外力F作用下的加速度．
次数 1 2 3 4 5
砝码盘中砝码的质量m/g 10 20 30 40 50
砝码盘中砝码的重力G/N 0.10 0.20 0.29 0.39 0.49
小车的加速度a/m?s-2 0.77 1.44 1.84 2.38 2.75
回答以下问题：
①按上述方案做实验，是否要求砝码和砝码盘的总质量远小于小车的质量？
 
（填“是”或“否”）．
②实验中打出的一条纸带如图3所示，由该纸带可求得小车的加速度a=
 
 m/s2．
③某同学将有关数据填人他所设计的表格中，并根据表中的数据画出a一F图象（如图4）．造成图线不过坐标原点的一条最主要原因是
 
，从该图线延长线与横轴的交点可求出的物理量是
 
，其大小是
 
．
精英家教网每年全国由于行人不遵守交通规则而引发的交通事故上万起，死亡上千人．只有科学设置交通管制，人人遵守交通规则，才能保证行人的生命安全．如图所示，停车线AB与前方斑马线边界CD间的距离为29m．质量8×103kg、车长7m的卡车以18m/s的速度向北匀速行驶，当卡车前端刚驶过停车线AB，该车前方的机动车交通信号灯由绿灯变黄灯．
（1）若此时前方C处人行横道路边等待的行人就抢先过马路，卡车司机发现行人，立即制动，卡车受到阻力做匀减速直线运动，阻力大小为2.4×104N．求卡车的制动距离；
（2）若人人遵守交通规则，该车将不受影响地驶过前方斑马线边界CD．为确保行人安全，D处人行横道信号灯应该在南北向机动车信号灯变黄灯后至少多久变为绿灯？
(1)某兴趣小组为测一遥控电动小车的额定功率，进行了如下实验：

①用天平测出电动小车的质量为0.4 kg；

②将电动小车、纸带和打点计时器按如图甲所示安装；

③接通打点计时器(其打点时间间隔为0.02 s)；

④使电动小车以额定功率加速运动，达到最大速度一段时间后关闭小车电源，待小车静止时再关闭打点计时器(设小车在整个过程中所受的阻力恒定)。

在上述过程中，打点计时器在纸带上所打的部分点迹如图乙所示(图中长度单位：cm)。

请你分析纸带数据，回答下列问题(结果均保留两位有效数字)：

①该电动小车运动的最大速度为____________m／s；

②该电动小车在匀减速运动的加速度大小为___________m／s2；

③该电动小车的额定功率为__________W。

(2)为了测量一个量程为3.0 V电压表的内阻Rv，(约几千欧)，某同学采用了如图所示的电路(部分实物电路已连好)，利用“半偏法”进行测量，电路中电阻箱R0的最大值为9 999 Ω，滑动变阻器R的最大阻值为50 Ω。

①按图示电路将所给的实物测量电路补充完整。

②该同学测量电压表的内阻时，其实验步骤为：

A.将电阻箱R0的阻值调到零                  B.闭合开关S

C.连接好电路，注意断开开关s              D.把滑动变阻器R的滑片P滑到b端

E.调节电阻箱R0的阻值，使电压表的示数为1.5 V

F.调节滑动变阻器R，使电压表的示数为3.0 V

G.记下此时电阻箱R0的阻值

以上实验步骤合理的顺序为__________。(填写字母)

③若所记电阻箱R0的阻值为3 500 Ω，则用此法测得的电压表内阻是___________kΩ。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网