题目内容
【题目】如图所示,斜面AB倾角为37°,底端A点与斜面上B点相距10m,甲、乙两物体大小不计,与斜面间的动摩擦因数为0.5,某时刻甲从A点沿斜面以10m/s的初速度滑向B,同时乙物体从B点无初速释放,(sin37°=0.6,cos37°=0.8,g=10m/s2)求:
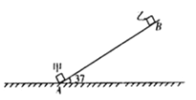
(1)甲物体沿斜面上滑、下滑的加速度大小;
(2)甲物体上滑的时间.
(3)甲、乙两物体经多长时间相遇.
【答案】(1)![]() ,
,![]() (2)t=1s (3)t总=3s
(2)t=1s (3)t总=3s
【解析】(1)滑块甲沿斜面向上运动时,加速度大小为![]()
根据牛顿第二定律和受力分析知
![]()
代入数据得:![]()
设滑块乙沿斜面向下运动时,加速度大小为![]()
![]()
代入数据得:![]()
(2)滑块甲向上做匀减速由运动学公式得:![]()
速度即减为零.,即甲上滑的时间为1s
(3)在甲上滑过程中甲向上的位移:![]()
物块乙在这段时间内下滑时的位移大小为:
![]() =
=![]()
此时二者之间的距离:![]()
乙的速度:![]()
说明二者还没有相遇,距离是4m两个物块与斜面之间的动摩擦因数相等,所以甲向下运动时的加速度大小也是![]() 两个物块都向下做匀加速运动,相对位移为
两个物块都向下做匀加速运动,相对位移为![]() ,设需要时间
,设需要时间![]() 即相遇
即相遇
由运动公式得;
![]() =
=![]()
解得:![]()
所以是乙追上甲,时间:![]()
综上所述本题答案是:
(1)甲物体沿斜面上滑的加速度大小是![]() ;(2)甲上滑的时间为1s (3)甲、乙两物体经3s时间相遇.
;(2)甲上滑的时间为1s (3)甲、乙两物体经3s时间相遇.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目