题目内容
20. 如图所示,A、B为半径分别是R、2R的同心轮,与半径为R的C轮用皮带传动,且不打滑,a、b、c分别为三轮边缘上的三个点,则这三个点的线速度之比为:2:1:2;这三个点的角速度之比为:1:1:2;这三个点的向心加速度之比为:2:1:4.
如图所示,A、B为半径分别是R、2R的同心轮,与半径为R的C轮用皮带传动,且不打滑,a、b、c分别为三轮边缘上的三个点,则这三个点的线速度之比为:2:1:2;这三个点的角速度之比为:1:1:2;这三个点的向心加速度之比为:2:1:4.
分析 两轮子靠传送带传动,轮子边缘上的点具有相同的线速度;共轴转动的点,具有相同的角速度;结合公式v=ωr和$a=\frac{{v}^{2}}{r}={ω}^{2}r$列式求解.
解答 解:已知A、B、C三轮的半径之间的关系是ra=2rb=2rc,故:ra:rb:rc=2:1:1;
①A、B两个轮子是同轴传动,角速度相等,故:ωa:ωb=1:1
根据公式v=ωr,线速度之比为:va:vb=ra:rb=2:1
根据公式a=ω2r,向心加速度之比为:aa:ab=2:1
②B、C两个轮子靠传送带传动,轮子边缘上的点具有相同的线速度,故:va:vc=1:1
根据公式v=ωr,角速度之比为:$\frac{{ω}_{a}}{{ω}_{c}}$=$\frac{{r}_{c}}{{r}_{a}}$=$\frac{1}{2}$
根据公式$a=\frac{{v}^{2}}{r}$得:向心加速度之比为:$\frac{{a}_{a}}{{a}_{c}}$=$\frac{{r}_{c}}{{r}_{a}}$=$\frac{1}{2}$
故:
ωa:ωb:ωc=1:1:2
va:vb:vc=2:1:2
aa:ab:ac=2:1:4
故答案为:2:1:2,1:1:2,2:1:4.
点评 本题关键抓住同缘传动边缘上的点线速度相等、同轴传动角速度相同以及线速度与角速度关系公式v=ωr列式求解.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
15.关于向心力的说法中正确的是( )
| A. | 物体由于做圆周运动而产生了一个指向圆心的力就是向心力 | |
| B. | 向心力不能改变做圆周运动物体的速度大小 | |
| C. | 做匀速圆周运动的物体,其向心力是不变的 | |
| D. | 做圆周运动的物体,其所受外力的合力的方向一定指向圆心 |
5.质量为0.2kg的小球做自由落体运动,在其下落过程中,第1s末重力做功的瞬时功率为 ;1s内重力做功的平均功率为 (g取10m/s2)( )
| A. | 10 W;10 W | B. | 15 W;15 W | C. | 20 W;10 W | D. | 25 W;15 W |
9. 某学生做观察电磁感应现象的实验,将电流表、线圈A和B、蓄电池、开关用导线接成如图所示的实验电路,当它闭合、断开开关时,电流表的指针都没有偏转,其原因是( )
某学生做观察电磁感应现象的实验,将电流表、线圈A和B、蓄电池、开关用导线接成如图所示的实验电路,当它闭合、断开开关时,电流表的指针都没有偏转,其原因是( )
 某学生做观察电磁感应现象的实验,将电流表、线圈A和B、蓄电池、开关用导线接成如图所示的实验电路,当它闭合、断开开关时,电流表的指针都没有偏转,其原因是( )
某学生做观察电磁感应现象的实验,将电流表、线圈A和B、蓄电池、开关用导线接成如图所示的实验电路,当它闭合、断开开关时,电流表的指针都没有偏转,其原因是( )| A. | 开关位置接错 | B. | 电流表的正、负接线柱接反 | ||
| C. | 线圈B的接头3、4接反 | D. | 蓄电池的正负极接反 |

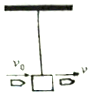 如图所示,用细线挂以质量为M的木块,有一质量为m的子弹自左向右水平射穿此木块,穿透前后子弹的速度分别为vo 和v(设子弹穿过木块的时间和空气阻力不计),求子弹穿出后木块上升的最大高度h.
如图所示,用细线挂以质量为M的木块,有一质量为m的子弹自左向右水平射穿此木块,穿透前后子弹的速度分别为vo 和v(设子弹穿过木块的时间和空气阻力不计),求子弹穿出后木块上升的最大高度h.