题目内容
如图7—10所示,倾角为30°的直角三角形底边长为2L,底边处在水平位置,斜边为光滑绝缘导轨。现在底边中点O处固定一正电荷Q,让一个质量为m带正电的点电荷q从斜面顶端A沿斜边滑下,(整个运动过程中始终不脱离斜面)已测得它滑到斜边上的垂足D处时速度为v,加速度为a,方向沿斜面向下,试求该质点滑到斜边底端C点时的速度和加速度各为多大?

1)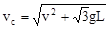 (2)
(2)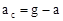
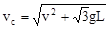 (2)
(2)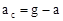
1)由图可知,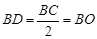 ,△BOD为等边三角形,可见B、C、D在同一个以O为圆心的圆周上,即点电荷Q的等势面上,故电荷q从O到C,电场力不做功,从D→C由动能定理
,△BOD为等边三角形,可见B、C、D在同一个以O为圆心的圆周上,即点电荷Q的等势面上,故电荷q从O到C,电场力不做功,从D→C由动能定理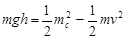 ,h=Bdsin60°Bcsin30°
,h=Bdsin60°Bcsin30°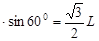 。
。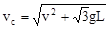
(2)设点电荷Q在D、C产生磁场场强为正,又设q在D点受力分析,产生加速度a,由牛顿第二定律F=mgsin30°-qEcos30°=ma,q在C点: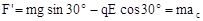 得:
得: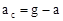
本题考查动能定理,由D到c时应用动能定理列公式求解,设点电荷Q在D、C产生磁场场强为正,又设q在D点受力分析,根据牛顿第二定律列式求解
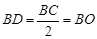 ,△BOD为等边三角形,可见B、C、D在同一个以O为圆心的圆周上,即点电荷Q的等势面上,故电荷q从O到C,电场力不做功,从D→C由动能定理
,△BOD为等边三角形,可见B、C、D在同一个以O为圆心的圆周上,即点电荷Q的等势面上,故电荷q从O到C,电场力不做功,从D→C由动能定理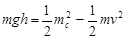 ,h=Bdsin60°Bcsin30°
,h=Bdsin60°Bcsin30°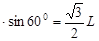 。
。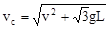
(2)设点电荷Q在D、C产生磁场场强为正,又设q在D点受力分析,产生加速度a,由牛顿第二定律F=mgsin30°-qEcos30°=ma,q在C点:
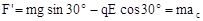 得:
得: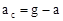
本题考查动能定理,由D到c时应用动能定理列公式求解,设点电荷Q在D、C产生磁场场强为正,又设q在D点受力分析,根据牛顿第二定律列式求解

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的初速度滑上小车左端,带动小车向右运动,小车跟墙壁碰撞时,滑块处在小车正中间位置且恰好与小车达到共同速度,碰后小车即被粘在墙壁上,滑块最终通过了半圆形轨道的最高点,已知滑块与小车表面的动摩擦因数片
的初速度滑上小车左端,带动小车向右运动,小车跟墙壁碰撞时,滑块处在小车正中间位置且恰好与小车达到共同速度,碰后小车即被粘在墙壁上,滑块最终通过了半圆形轨道的最高点,已知滑块与小车表面的动摩擦因数片


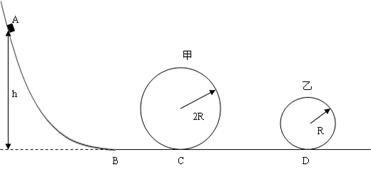
 ,则小物体下滑到斜面底端B时的速度 m/s及所用时间 s.(g取10 m/s2)
,则小物体下滑到斜面底端B时的速度 m/s及所用时间 s.(g取10 m/s2)

 ,探测器一定能到达月球
,探测器一定能到达月球