题目内容
4. 如图所示,在光滑水平地面上静止放置由弹簧相连接的两木块A和B,一质量为m的子弹以水平速度v0击中木块A,子弹没有穿出.已知A的质量mA=m,B的质量mB=2m.求:
如图所示,在光滑水平地面上静止放置由弹簧相连接的两木块A和B,一质量为m的子弹以水平速度v0击中木块A,子弹没有穿出.已知A的质量mA=m,B的质量mB=2m.求:(1)A的最大速度
(2)求弹簧的最大弹性势能.
分析 (1)子弹击中A后的瞬间A的速度最大,子弹与A组成的系统动量守恒,由动量守恒定律可以求出A的最大速度;
(2)子弹、A、B组成的系统动量守恒,当它们速度相等时弹簧的压缩量最大,弹簧的弹性势能最大,由动量守恒定律与能量守恒定律求出弹簧的最大弹性势能.
解答 解:(1)子弹与A组成的系统动量守恒,以子弹的初速度方向为正方向,由动量守恒定律得:
mv0=(m+mvA)v,解得A的最大速度:v=$\frac{1}{2}$v0;
(2)子弹、A、B组成的系统动量守恒,以向右为正方向,由动量守恒定律得:
mv0=(m+mA+mB)v′,
解得:v′=$\frac{1}{4}$v0,
由能量守恒定律得:$\frac{1}{2}$(m+mA)v2=EP+$\frac{1}{2}$(m+mA+mB)v′2,
解得:EP=$\frac{1}{8}$mv02;
答:(1)A的最大速度为$\frac{1}{2}$v0;
(2)弹簧的最大弹性势能为$\frac{1}{8}$mv02.
点评 本题考查了求速度、弹性势能问题,分析清楚物体运动过程是正确解题的关键,应用动量守恒定律与能量守恒定律即可解题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
15. 如图所示,实线为一电场中的等势面,是中心对称图形.a、b、c、d是以中心点为圆心的圆周上的四个点,则下列说法中正确的是( )
如图所示,实线为一电场中的等势面,是中心对称图形.a、b、c、d是以中心点为圆心的圆周上的四个点,则下列说法中正确的是( )
 如图所示,实线为一电场中的等势面,是中心对称图形.a、b、c、d是以中心点为圆心的圆周上的四个点,则下列说法中正确的是( )
如图所示,实线为一电场中的等势面,是中心对称图形.a、b、c、d是以中心点为圆心的圆周上的四个点,则下列说法中正确的是( )| A. | a、b、c、d四点电势不等,但电场强度相等 | |
| B. | 若一电子从b点运动到c点,克服电场力做的功为0.4eV | |
| C. | 若一电子从左侧沿中心轴线穿越电场区域,将做加速度先增加后减小的加速直线运动 | |
| D. | 若一束电子从左侧平行于中心轴线进入电场区域,将会从右侧平行于中心轴线穿出 |
9.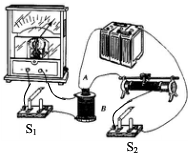 如图所示,螺线管B套在螺线管A外边,螺线管A经过滑动变阻器和开关S2与电源相连接构成直流闭合电路;螺线管B与开关S1、灵敏电流计构成另一闭合回路.进行下列操作,没有产生电磁感应现象的是( )
如图所示,螺线管B套在螺线管A外边,螺线管A经过滑动变阻器和开关S2与电源相连接构成直流闭合电路;螺线管B与开关S1、灵敏电流计构成另一闭合回路.进行下列操作,没有产生电磁感应现象的是( )
 如图所示,螺线管B套在螺线管A外边,螺线管A经过滑动变阻器和开关S2与电源相连接构成直流闭合电路;螺线管B与开关S1、灵敏电流计构成另一闭合回路.进行下列操作,没有产生电磁感应现象的是( )
如图所示,螺线管B套在螺线管A外边,螺线管A经过滑动变阻器和开关S2与电源相连接构成直流闭合电路;螺线管B与开关S1、灵敏电流计构成另一闭合回路.进行下列操作,没有产生电磁感应现象的是( )| A. | 闭合S1,接通S2的瞬间 | |
| B. | 闭合S1和S2,断开S2的瞬间 | |
| C. | 闭合S1和S2,断开S1的瞬间 | |
| D. | 断开S1,闭合S2,滑动滑动变阻器滑片的过程中 |
16.在LC电磁振荡回路中,电容两端的电压u随时间t变化的规律如图所示,则( )


| A. | 在时刻t1,电路中的磁场能最小 | |
| B. | 在时刻t2,电路中的磁场能最小 | |
| C. | 从时刻t2至t3,在电路中磁场能转化为电场能 | |
| D. | 从时刻t2至t3,在电路中电场能转化为磁场能 |
13. 如图,高为h的光滑平面上有一质量为m的物块,用绳子跨过定滑轮由地面上的人以速度V0向右拉动,当人从平面的边缘处向右匀速前进了S的距离(不计人身高,不计绳的质量以及绳与滑轮间的摩擦力),则( )
如图,高为h的光滑平面上有一质量为m的物块,用绳子跨过定滑轮由地面上的人以速度V0向右拉动,当人从平面的边缘处向右匀速前进了S的距离(不计人身高,不计绳的质量以及绳与滑轮间的摩擦力),则( )
 如图,高为h的光滑平面上有一质量为m的物块,用绳子跨过定滑轮由地面上的人以速度V0向右拉动,当人从平面的边缘处向右匀速前进了S的距离(不计人身高,不计绳的质量以及绳与滑轮间的摩擦力),则( )
如图,高为h的光滑平面上有一质量为m的物块,用绳子跨过定滑轮由地面上的人以速度V0向右拉动,当人从平面的边缘处向右匀速前进了S的距离(不计人身高,不计绳的质量以及绳与滑轮间的摩擦力),则( )| A. | 在该过程中,物块也做匀速运动 | B. | 人对物块做功$\frac{1}{2}$mv02 | ||
| C. | 人对物块做功$\frac{{m{V_0}^2{S^2}}}{{2({h^2}+{S^2})}}$ | D. | 物块运动的速率为$\frac{{{V_0}h}}{{\sqrt{{h^2}+{S^2}}}}$ |
14.物理学发展的过程中,许多物理学家的科学发现推动了人类历史的进步.以下叙述中,正确的说法是( )
| A. | 开普勒发现万有引力定律 | |
| B. | 爱因斯坦提出:在一切惯性参照物中,测量到的真空中的光速c都一样 | |
| C. | 牛顿利用扭秤实验,首先测出引力常量,为人类实现飞天梦想奠定了基础 | |
| D. | 相对论的创立表明经典物理学已不再适用 |
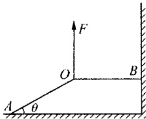 如图所示,一根细绳一端系于水平地面上,另一端系于竖直墙壁上,在绳上O点处竖直向上加一个拉力大小为F,OA与水平面夹角为θ,绳OB垂直于墙壁,此时处于平衡状态.
如图所示,一根细绳一端系于水平地面上,另一端系于竖直墙壁上,在绳上O点处竖直向上加一个拉力大小为F,OA与水平面夹角为θ,绳OB垂直于墙壁,此时处于平衡状态. 如图所示,飞机离地面高度为H=500m,飞机的水平飞行速度为v1=100m/s,追击一辆速度为v2=20m/s同向行驶的汽车,欲使炸弹击中汽车.求:
如图所示,飞机离地面高度为H=500m,飞机的水平飞行速度为v1=100m/s,追击一辆速度为v2=20m/s同向行驶的汽车,欲使炸弹击中汽车.求: