��Ŀ����
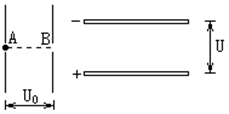
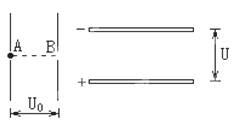
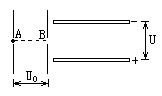
��ͼ��ʾΪ����ƽ�а�����壬һ����ֱ���ã�һ��ˮƽ���ã�����һ����Ϊm�ĵ���Ϊe�ĵ��Ӿ�ֹ����ֱ���õ�ƽ�н������A�㣬����ѹU0���ٺ�ͨ��B�����������Ϊd����ѹΪU��ˮƽ���õ�ƽ�н�����䣬�����Ӵ�����ˮƽƽ�а�����м����룬�������Ӹպ��ܴ��Ҳ������ƽ�н����崩����A��B�ֱ�Ϊ������ֱ����е㣬��
1.����ͨ��B��ʱ���ٶȴ�С
2.�Ҳ�ƽ�н�����ij���
3.���Ӵ����Ҳ�ƽ�н�����ʱ�Ķ��ܺ��ٶȷ���
1.
2.
3.
����:��1���ɶ��ܶ��� e U0=mv02/2��v0= (3��)
��2�����ӽ���ƫת�糡����ƽ���˶�����峤ΪL
L=v0 t (1��)
y=d/2=at2/2 (2��)
a=F/m= eU/md (2��)
�������ϵ�L= (2��)
��3��ȫ�����ɶ��ܶ��� eU0+ eU= EK -0 ��EK = eU0+
eU (2��)
�ٶȷ�����ˮƽ����нǦ����� tan��=at/ v0=

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
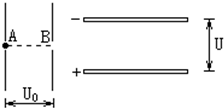 ��ͼ��ʾΪ����ƽ�а�����壬һ����ֱ���ã�һ��ˮƽ���ã�����һ����Ϊm�ĵ��Ӿ�ֹ����ֱ���õ�ƽ�н������A�㣬����ѹU0���ٺ�ͨ��B�����������Ϊd����ѹΪU��ˮƽ���õ�ƽ�н�����䣬�����Ӵ�����ˮƽƽ�а�����м����룬�������Ӹպ��ܴ��Ҳ������ƽ�н����崩����A��B�ֱ�Ϊ������ֱ����е㣬��
��ͼ��ʾΪ����ƽ�а�����壬һ����ֱ���ã�һ��ˮƽ���ã�����һ����Ϊm�ĵ��Ӿ�ֹ����ֱ���õ�ƽ�н������A�㣬����ѹU0���ٺ�ͨ��B�����������Ϊd����ѹΪU��ˮƽ���õ�ƽ�н�����䣬�����Ӵ�����ˮƽƽ�а�����м����룬�������Ӹպ��ܴ��Ҳ������ƽ�н����崩����A��B�ֱ�Ϊ������ֱ����е㣬��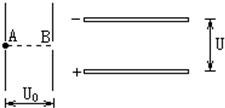 ��ͼ��ʾΪ����ƽ�а�����壬һ����ֱ���ã�һ��ˮƽ���ã�����һ����Ϊm�ĵ���Ϊe�ĵ��Ӿ�ֹ����ֱ���õ�ƽ�н������A�㣬����ѹU0���ٺ�ͨ��B�����������Ϊd����ѹΪU��ˮƽ���õ�ƽ�н�����䣬�����Ӵ�����ˮƽƽ�а�����м����룬�������Ӹպ��ܴ��Ҳ������ƽ�н����崩����A��B�ֱ�Ϊ������ֱ����е㣬��
��ͼ��ʾΪ����ƽ�а�����壬һ����ֱ���ã�һ��ˮƽ���ã�����һ����Ϊm�ĵ���Ϊe�ĵ��Ӿ�ֹ����ֱ���õ�ƽ�н������A�㣬����ѹU0���ٺ�ͨ��B�����������Ϊd����ѹΪU��ˮƽ���õ�ƽ�н�����䣬�����Ӵ�����ˮƽƽ�а�����м����룬�������Ӹպ��ܴ��Ҳ������ƽ�н����崩����A��B�ֱ�Ϊ������ֱ����е㣬��