题目内容
8.甲车以10米/秒,乙车以4米/秒的速率在同一直车道中同向前进,若甲车驾驶员在乙车后方距离d处发现乙车,立即踩刹车使其车获得2米/秒2的加速度,为使两车不致相撞,d的值至少应为( )| A. | 3米 | B. | 9米 | C. | 16米 | D. | 20米 |
分析 速度大者减速追速度小者,当速度相等时,距离最小,抓住速度相等时恰好追上,结合位移公式求出d的最小值.
解答 解:当甲乙速度相等时,所经历的时间t=$\frac{{v}_{甲}-{v}_{乙}}{a}$=$\frac{10-4}{2}$s=3s.
根据位移关系得,$\frac{{{v}_{甲}}^{2}-{{v}_{乙}}^{2}}{2a}={v}_{乙}t+d$
代入数据解得d=9m.知d的最小值为9m.故B正确,A、C、D错误.
故选:B.
点评 解决本题的关键抓住临界情况,即速度相等时恰好追上,结合位移关系进行求解.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
18.一实验小组准备探究某种元件Q的伏安特性曲线,他们设计了如图1所示的电路图.请回答下列问题:

(1)请将图2中的实物连线按电路图补充完整.
(2)考虑电表内阻的影响,该元件电阻的测量值小于(选填“大于”、“等于”或“小于”)真实值.
(3)在电路图中闭合开关S,电流表、电压表均有示数,但无论怎样移动变阻器滑动片,总不能使电压表的示数调为零.原因可能是图中的f(选填a、b、c、d、e、f)处接触不良.
(4)实验测得表格中的7组数据.请在图3坐标纸上作出该元件的I-U图线.
(5)为了求元件Q在I-U图线上某点的电阻,甲同学利用该点的坐标I、U,由R=$\frac{U}{I}$求得.乙同学作出该点的切线,求出切线的斜率k,由R=$\frac{1}{k}$求得.其中甲(选填“甲”、“乙”)同学的方法正确.

(1)请将图2中的实物连线按电路图补充完整.
(2)考虑电表内阻的影响,该元件电阻的测量值小于(选填“大于”、“等于”或“小于”)真实值.
(3)在电路图中闭合开关S,电流表、电压表均有示数,但无论怎样移动变阻器滑动片,总不能使电压表的示数调为零.原因可能是图中的f(选填a、b、c、d、e、f)处接触不良.
(4)实验测得表格中的7组数据.请在图3坐标纸上作出该元件的I-U图线.
| 序号 | 电压/V | 电流/A |
| 1 | 0.00 | 0.00 |
| 2 | 0.40 | 0.02 |
| 3 | 0.80 | 0.05 |
| 4 | 1.20 | 0.12 |
| 5 | 1.60 | 0.20 |
| 6 | 2.00 | 0.31 |
| 7 | 2.40 | 0.44 |
19.关于经典时空观和相对论时空观,下列说法中错误的是( )
| A. | 经典时空观认为时间和空间是独立于物体及其运动而存在的 | |
| B. | 相对论时空观认为时间和空间与物体及其运动有关系 | |
| C. | 经典力学只适用于宏观物体、低速运动问题,不适用于高速运动的问题 | |
| D. | 当物体的运动速度远小于光速时,关于物体的运动相对论和经典力学的结论仍有很大的区别 |
16.下列关于平均速度、瞬时速度、平均速率的说法中正确的是( )
| A. | 平均速度$\overline{v}$=$\frac{△x}{△t}$,当△t充分小时,该式可表示t时刻的瞬时速度 | |
| B. | 匀速直线运动的平均速度不等于瞬时速度 | |
| C. | 瞬时速度和平均速度都可以精确描述变速运动 | |
| D. | 平均速度的大小就是平均速率 |
3.如图所示,物体A靠在竖直墙面上,在力F作用下,A、B保持静止.物体A的受力个数为( )
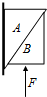

| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
13.为了减小实验误差,以下操作中不必要的是( )
| A. | 在“研究匀变速直线运动”的实验中,供小车运动的平板应光滑 | |
| B. | 在“验证力的平行四边形定则”的实验中,弹簧测力计必须与木板平行,读数时视线要正对弹簧测力计的刻度 | |
| C. | 用落体法验证机械能守恒定律时,必需选择纸带上的第一打点为起始点 | |
| D. | 在“探究弹簧弹力与伸长量的关系”实验中,弹簧竖直悬挂状态下测出弹簧原长 |
20. 如图所示,理想变压器原副线圈匝数比为10:1,电源电压u=220$\sqrt{2}$sin100πt(V),通过电阻R0接在变压器原线圈两端,开关闭合后,电压表示数为12V,电流表的示数为10A.以下说法正确的是( )
如图所示,理想变压器原副线圈匝数比为10:1,电源电压u=220$\sqrt{2}$sin100πt(V),通过电阻R0接在变压器原线圈两端,开关闭合后,电压表示数为12V,电流表的示数为10A.以下说法正确的是( )
 如图所示,理想变压器原副线圈匝数比为10:1,电源电压u=220$\sqrt{2}$sin100πt(V),通过电阻R0接在变压器原线圈两端,开关闭合后,电压表示数为12V,电流表的示数为10A.以下说法正确的是( )
如图所示,理想变压器原副线圈匝数比为10:1,电源电压u=220$\sqrt{2}$sin100πt(V),通过电阻R0接在变压器原线圈两端,开关闭合后,电压表示数为12V,电流表的示数为10A.以下说法正确的是( )| A. | R0的阻值是100Ω | B. | 电源的功率是120W | ||
| C. | 若将开关断开,电压表的示数是22V | D. | 副线圈中电流的频率是100Hz |
18. 如图所示,a、b是真空中两个等量异种点电荷,A、B为两点电荷连线中垂线上的两点.现将一正点电荷q由A点沿中垂线移到B点,下列说法中正确的是( )
如图所示,a、b是真空中两个等量异种点电荷,A、B为两点电荷连线中垂线上的两点.现将一正点电荷q由A点沿中垂线移到B点,下列说法中正确的是( )
 如图所示,a、b是真空中两个等量异种点电荷,A、B为两点电荷连线中垂线上的两点.现将一正点电荷q由A点沿中垂线移到B点,下列说法中正确的是( )
如图所示,a、b是真空中两个等量异种点电荷,A、B为两点电荷连线中垂线上的两点.现将一正点电荷q由A点沿中垂线移到B点,下列说法中正确的是( )| A. | A点电势大于B点电势 | |
| B. | A点电场强度大于B点的电场强度 | |
| C. | 电荷在A的电势能等于在B点的电势能 | |
| D. | 电荷移动过程中,加速度可能先增大后减小 |
 如图所示,水平桌面上固定一个曲面体A,其底端切线是水平的.一个可看作质点的滑块B.现在提供的实验测量工具只有天平、直尺.请设计一个实验,测出滑块B自斜面顶端由静止下滑到底端过程中,滑块B克服摩擦力所做的功.(另外手头还有白纸、复写纸、胶带和圆规等)
如图所示,水平桌面上固定一个曲面体A,其底端切线是水平的.一个可看作质点的滑块B.现在提供的实验测量工具只有天平、直尺.请设计一个实验,测出滑块B自斜面顶端由静止下滑到底端过程中,滑块B克服摩擦力所做的功.(另外手头还有白纸、复写纸、胶带和圆规等)