题目内容
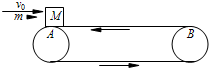 (2007?武清区模拟)如图所示,水平传送带AB足够长,质量为M=1kg的木块随传送带一起以v1=2m/s的速度向左匀速运动(传送带的速度恒定),木块与传送带的动摩擦因数μ=0.5,当木块运动到最左端A点时,一颗质量为m=20g的子弹,以v0=300m/s的水平向右的速度,正对射入木块并穿出,穿出速度v=50m/s,设子弹射穿木块的时间极短,(g取10m/s2)求:
(2007?武清区模拟)如图所示,水平传送带AB足够长,质量为M=1kg的木块随传送带一起以v1=2m/s的速度向左匀速运动(传送带的速度恒定),木块与传送带的动摩擦因数μ=0.5,当木块运动到最左端A点时,一颗质量为m=20g的子弹,以v0=300m/s的水平向右的速度,正对射入木块并穿出,穿出速度v=50m/s,设子弹射穿木块的时间极短,(g取10m/s2)求:(1)木块遭射击后远离A的最大距离;
(2)木块遭击后到相对传送带静止所经历的时间.
分析:(1)根据动量守恒定律求出木块遭射击后瞬间的速度,再根据动能定理求出速度减为零的距离,该距离为远离A的最大距离.
(2)木块先向右做匀减速直线运动到零,返回做匀加速直线运动,当速度达到和传送带速度相同时,一起做匀速直线运动,根据牛顿第二定律结合运动学公式求出木块遭击后到相对传送带静止所经历的时间.
(2)木块先向右做匀减速直线运动到零,返回做匀加速直线运动,当速度达到和传送带速度相同时,一起做匀速直线运动,根据牛顿第二定律结合运动学公式求出木块遭击后到相对传送带静止所经历的时间.
解答:解:(1)设木块遭射击后的速度瞬间变为V,以水平向右为正方向,根据动量守恒定律得,
mv0-Mv1=mv+MV
则V=
-v1,代入数据解得V=3m/s,方向向右.
木块遭击后沿传送带向右匀减速滑动.
摩擦力f=μFN=μMg=5N
设木块远离A点的最大距离为S,此时木块的末速度为0.
根据动能定理得,-fs=0-
MV2
则s=
=
m=0.9m.
(2)木块遭击后沿传送带向右匀减速滑动,加速度a1=
=μg=5m/s2
经历时间t1=
=
=0.6s
木块在传送带上向左加速运动一段时间t2之后速度达到2m/s,与传送带相对静止.a2=
=μgt2═
=0.4
所求时间 t=t1+t2=0.6+0.4=1.0s
答:(1)木块遭射击后远离A的最大距离为0.9m.
(2)木块遭击后到相对传送带静止所经历的时间为1.0s.
mv0-Mv1=mv+MV
则V=
| m(v0-v) |
| M |
木块遭击后沿传送带向右匀减速滑动.
摩擦力f=μFN=μMg=5N
设木块远离A点的最大距离为S,此时木块的末速度为0.
根据动能定理得,-fs=0-
| 1 |
| 2 |
则s=
| MV2 |
| 2f |
| 1×32 |
| 2×5 |
(2)木块遭击后沿传送带向右匀减速滑动,加速度a1=
| f |
| M |
经历时间t1=
| V |
| a |
| 3 |
| 5 |
木块在传送带上向左加速运动一段时间t2之后速度达到2m/s,与传送带相对静止.a2=
| f |
| M |
| 2 |
| 5 |
所求时间 t=t1+t2=0.6+0.4=1.0s
答:(1)木块遭射击后远离A的最大距离为0.9m.
(2)木块遭击后到相对传送带静止所经历的时间为1.0s.
点评:本题综合考查了动量守恒定律、动能定理、牛顿第二定律以及运动学公式,关键理清运动过程,选择合适的规律进行求解.

练习册系列答案
相关题目
 (2007?居巢区模拟)如图所示,结点O在三个力作用下平衡,保持θ不变,将B点向上移,则BO绳的拉力将( )
(2007?居巢区模拟)如图所示,结点O在三个力作用下平衡,保持θ不变,将B点向上移,则BO绳的拉力将( ) (2007?武清区模拟)一个正方形线圈边长a=0.20m,共有n=100匝,其总电阻r=4.0Ω.线圈与阻值R=16Ω的外电阻连成闭合回路,如图甲所示.线圈所在区域存在着分布均匀但强弱随时间变化的磁场,磁场方向垂直线圈平面,其磁感应强度B的大小随时间作周期性变化的周期T=1.0×10-2s,如图乙所示,图象中
(2007?武清区模拟)一个正方形线圈边长a=0.20m,共有n=100匝,其总电阻r=4.0Ω.线圈与阻值R=16Ω的外电阻连成闭合回路,如图甲所示.线圈所在区域存在着分布均匀但强弱随时间变化的磁场,磁场方向垂直线圈平面,其磁感应强度B的大小随时间作周期性变化的周期T=1.0×10-2s,如图乙所示,图象中 (2007?武清区模拟)如图所示,一边长为h的正方形线圈A,其电流I大小方向均固定不变,用两条长度恒为h的细绳静止悬挂于水平长直导线CD的正下方.当导线CD中无电流时,两细绳中张力均为T,当通过CD的电流为i1时,两细绳中张力均降为aT(0<a<1=,而当CD上的电流为i2时,细绳中张力恰好为零.已知长直通电导线的磁场的磁感应强度B与电流强度成正比,与场点到导线的距离r成反比(即B=ki/r,k为常数).由此可知,CD中的电流方向和电流之比i1/i2分别为( )
(2007?武清区模拟)如图所示,一边长为h的正方形线圈A,其电流I大小方向均固定不变,用两条长度恒为h的细绳静止悬挂于水平长直导线CD的正下方.当导线CD中无电流时,两细绳中张力均为T,当通过CD的电流为i1时,两细绳中张力均降为aT(0<a<1=,而当CD上的电流为i2时,细绳中张力恰好为零.已知长直通电导线的磁场的磁感应强度B与电流强度成正比,与场点到导线的距离r成反比(即B=ki/r,k为常数).由此可知,CD中的电流方向和电流之比i1/i2分别为( )