题目内容
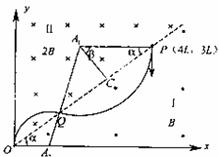
如图,在空间中有一坐标系xoy,其第一象限内充满着两个匀强磁场区域I和II,直线OP是它们的边界,区域I中的磁感应强度为B,方向垂直纸面向外;区域II中的磁感应强度为2B,方向垂直纸面向内,边界上的P点坐标为(4L,3L)。一质量为m,电荷量为q的带正粒子从P点平行于y轴负方向射入区域I,经过一段时间后,粒子恰好经过原点O,忽略粒子重力,已知sin37°=0.6,cos37°=0.8.求:

(1)粒子从P点运动到O点的时间至少为多少?
(2)粒子的速度大小可能是多少?
(1)设粒子的入射速度为v,用R1,R2,T1,T2分别表示粒子在磁场I区和II区中运动的轨道半径和周期。则
![]() ①
①
![]() ②
②
![]() ③
③
![]() ④
④
粒子先在磁场I区中做顺时针的圆周运动,后在磁场II区中做逆时针的圆周运动,然后从O点射出,这样料子从P点运动到O点所用的时间最短.
粒子运动轨迹如图所示.
![]()
![]()
粒子在磁场I区和II区中的运动时间分别为
![]()
![]()
粒子从P点运动到O点的时间至少为 t=t1+t2 ⑨
![]()
(2)粒子的速度大小满足一定条件时,粒子先在磁场I区中运动,后在磁场II区中运动,然后又重复前面的运动,直到经过原点O.这样粒子经过n个周期性的运动到过O点,每个周期的运动情况相同,
粒子在一个周期内的位移为
![]()
粒子每次在磁场I区中运动的位移为![]()
由图中几何关系可知![]()
由以上各式解得粒子的速度大小为![]() (n=1、2,3,……)
(n=1、2,3,……)

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2009?茂名二模)如图所示,位于竖直平面内的坐标系xoy,在其第三象限空间有沿水平方向的、垂直于纸面向外的匀强磁场,磁感应强度大小为B,还有沿x轴负方向的匀强电场,场强大小为E.在其第一象限空间有沿y轴负方向的、场强为
(2009?茂名二模)如图所示,位于竖直平面内的坐标系xoy,在其第三象限空间有沿水平方向的、垂直于纸面向外的匀强磁场,磁感应强度大小为B,还有沿x轴负方向的匀强电场,场强大小为E.在其第一象限空间有沿y轴负方向的、场强为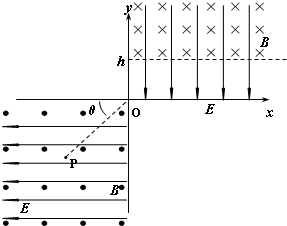 如图所示,位于竖直平面内的坐标系xoy,在其第三象限空间有沿水平方向的、垂直于纸面向外的匀强磁场,磁感应强度大小为B=0.5T,还有沿x轴负方向的匀强电场,场强大小为E=
如图所示,位于竖直平面内的坐标系xoy,在其第三象限空间有沿水平方向的、垂直于纸面向外的匀强磁场,磁感应强度大小为B=0.5T,还有沿x轴负方向的匀强电场,场强大小为E= 如图所示,位于竖直平面内的坐标系xOy,在其第三象限空间有沿水平方向的、垂直于纸面向外的匀强磁场,磁感应强度大小为B,还有沿x轴负方向的匀强电场,场强大小为E.在其第一象限空间有沿y轴负方向的、场强为E/ =4/3E的匀强电场,并在y >h区域有磁感应强度也为B的垂直于纸面向里的匀强磁场.一个带电荷量为q的油滴从图中第三象限的P点得到一初速度,恰好能沿PO作直线运动(PO与x轴负方向的夹角为θ =37°),并从原点O进入第一象限.已知重力加速度为g,sin37°= 0.6,cos37°= 0.8,问:
如图所示,位于竖直平面内的坐标系xOy,在其第三象限空间有沿水平方向的、垂直于纸面向外的匀强磁场,磁感应强度大小为B,还有沿x轴负方向的匀强电场,场强大小为E.在其第一象限空间有沿y轴负方向的、场强为E/ =4/3E的匀强电场,并在y >h区域有磁感应强度也为B的垂直于纸面向里的匀强磁场.一个带电荷量为q的油滴从图中第三象限的P点得到一初速度,恰好能沿PO作直线运动(PO与x轴负方向的夹角为θ =37°),并从原点O进入第一象限.已知重力加速度为g,sin37°= 0.6,cos37°= 0.8,问: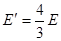 的匀强电场,并在y>h区域有磁感应强度也为B的垂直于纸面向里的匀强磁场。一个带电荷量为q的油滴从图中第三象限的P点得到一初速度,恰好能沿PO作直线运动(PO与x轴负方向的夹角为θ=37 o),并从原点O进入第一象限。已知重力加速度为g,sin37o=0.6,cos37o=0.8,求:
的匀强电场,并在y>h区域有磁感应强度也为B的垂直于纸面向里的匀强磁场。一个带电荷量为q的油滴从图中第三象限的P点得到一初速度,恰好能沿PO作直线运动(PO与x轴负方向的夹角为θ=37 o),并从原点O进入第一象限。已知重力加速度为g,sin37o=0.6,cos37o=0.8,求: