题目内容
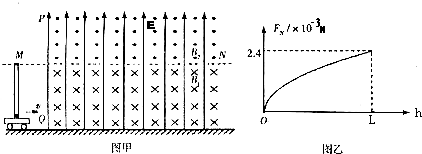
(2012?湖南模拟)如图甲所示,水平地面上有一辆小车,小车上固定有竖直光滑绝缘管,管长为L,管内底部有一质量m=0.2g,电荷量q=+8×10-5C的小球,小球的直径比管的内径略小.在管口所在水平面MN的下方存在着垂直纸面向里、磁感应强度B1=15T的匀强磁场,MN面上方存在着垂直纸面向外、磁感应强度B2=15T的匀强磁场,MN上下的整个区域还存在着竖直向上、场强E=25V/m的匀强电场.现让小车始终保持v=2m/s的速度匀速向右运动,以带电小球刚经过场的边界PQ为计时的起点,测得小球对管侧壁的弹力FN随小球到管底的高度h的变化关系如图乙所示.g取10m/s2,不计空气阻力.求:
(1)小球刚进入磁场B1时的加速度大小a;
(2)绝缘管的长度L;
(3)小球离开管后每次经过水平面MN时小球距管口的距离△x.
(1)小球刚进入磁场B1时的加速度大小a;
(2)绝缘管的长度L;
(3)小球离开管后每次经过水平面MN时小球距管口的距离△x.

分析:(1)小球在水平方向上随小车做匀速直线运动,刚进入磁场时,在竖直方向上对小球受力分析,受到竖直向下的重力和竖直向上的电场力以及洛伦兹力,在竖直方向上利用牛顿第二定律可求出小球的加速度.
(2)在小球刚要离开管口时,在水平方向上合力为零,在水平方向上受管侧壁的弹力和洛伦兹力(此力是速度在竖直方向上的分量产生的)结合牛顿运动定律和运动学公式可求出绝缘管的长度.
(3)当小球离开管口进入复合场时,对其受力分析,受到重力、电场力和洛伦兹力,经计算可判断重力和电场力平衡,可知小球会在洛伦兹力的作用下做匀速圆周运动,做出小球的运动轨迹图,利用有边界磁场的运动规律可求出小球和管口在水平方向上的位移之差.
(2)在小球刚要离开管口时,在水平方向上合力为零,在水平方向上受管侧壁的弹力和洛伦兹力(此力是速度在竖直方向上的分量产生的)结合牛顿运动定律和运动学公式可求出绝缘管的长度.
(3)当小球离开管口进入复合场时,对其受力分析,受到重力、电场力和洛伦兹力,经计算可判断重力和电场力平衡,可知小球会在洛伦兹力的作用下做匀速圆周运动,做出小球的运动轨迹图,利用有边界磁场的运动规律可求出小球和管口在水平方向上的位移之差.
解答:解:
(1)小球在管内运动时,以小球为研究对象,小球受到竖直向下的重力、竖直向上的电场力和大小恒定、方向竖直向上的洛伦兹力,设加速度为a,由牛顿第二定律有:
qB1v+qE-mg=ma
则:a=
=12m/s2;
(2)小球在管中竖直方向做匀加速直线运动,在小球运动到管口时,FN=2.4×10-3N,设v1为小球竖直分速度,水平方向有:
FN-qv1B1=0
解得:v1=
=2m/s
竖直方向有:v12=2aL
解得:L=
=
m
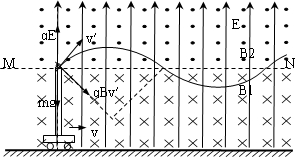
(3)小球离开管口进入复合场,小球受到竖直向下的重力、竖直向上的电场力和方向随时发生变化的洛伦兹力,
其中:
qE=8×10-5×25=2×10-3N
mg=0.2×10-3×10=2×10-3N
有qE=mg,故电场力与重力平衡,小球在复合场中做匀速圆周运动,合速度v'与MN成45°角,轨道半径为R,(如图)qvB2=
R=
=
m
小球离开管口开始计时,到再次经过MN所通过的水平距离
x1=2Rsin45°=
R=
m
T=
=
对应的时间有:
t=
T=
=
s
设小车运动的距离为x2
x2=vt=2×
=
s
若小球再经过MN时,有:
△x=n(x1-x2)
解得:△x=
(2-
)m n=1、2、3、…
答:(1)小球刚进入磁场B1时的加速度大小为12m/s2
(2)绝缘管的长度为
m
(3)小球离开管后每次经过水平面MN时小球距管口的距离为△x=
(2-
)m n=1、2、3、…
(1)小球在管内运动时,以小球为研究对象,小球受到竖直向下的重力、竖直向上的电场力和大小恒定、方向竖直向上的洛伦兹力,设加速度为a,由牛顿第二定律有:
qB1v+qE-mg=ma
则:a=
| qB1v+Eq-mg |
| m |
(2)小球在管中竖直方向做匀加速直线运动,在小球运动到管口时,FN=2.4×10-3N,设v1为小球竖直分速度,水平方向有:
FN-qv1B1=0
解得:v1=
| FN |
| qB1 |
竖直方向有:v12=2aL
解得:L=
| ||
| 2a |
| 1 |
| 6 |
(3)小球离开管口进入复合场,小球受到竖直向下的重力、竖直向上的电场力和方向随时发生变化的洛伦兹力,
其中:
qE=8×10-5×25=2×10-3N
mg=0.2×10-3×10=2×10-3N
有qE=mg,故电场力与重力平衡,小球在复合场中做匀速圆周运动,合速度v'与MN成45°角,轨道半径为R,(如图)qvB2=
| mv′2 |
| R |

R=
| mv′ |
| qB2 |
| ||
| 3 |
小球离开管口开始计时,到再次经过MN所通过的水平距离
x1=2Rsin45°=
| 2 |
| 2 |
| 3 |
T=
| 2πR |
| v′ |
| 2πm |
| qB2 |
对应的时间有:
t=
| 1 |
| 4 |
| πm |
| 2qB2 |
| π |
| 12 |
设小车运动的距离为x2
x2=vt=2×
| π |
| 12 |
| π |
| 6 |
若小球再经过MN时,有:
△x=n(x1-x2)
解得:△x=
| n |
| 3 |
| π |
| 2 |
答:(1)小球刚进入磁场B1时的加速度大小为12m/s2
(2)绝缘管的长度为
| 1 |
| 6 |
(3)小球离开管后每次经过水平面MN时小球距管口的距离为△x=
| n |
| 3 |
| π |
| 2 |
点评:该题考查了带电粒子在复合场中的运动,对复合场的理解和运动过程的分析是解决此类问题的关键.
复合场:即在同一区域内同时有电场、磁场和重力场,此类问题看似简单,受力也不复杂,但仔细分析其运动往往比较难以把握.
带电粒子在复合场中运动的分析方法和一般思路:
①当带电粒子所受合外力为零时,将做匀速直线运动或处于静止状态.合外力恒定且与初速同向时做匀变速直线运动,常见的情况有:
Ⅰ、洛伦兹力为零(即v∥B),重力与电场力平衡,做匀速直线运动;或重力与电场力的合力恒定,做匀变速运动.
Ⅱ、洛伦兹力f洛与重力和电场力的合力平衡,做匀速直线运动.
②带电粒子所受合外力做向心力,带电粒子做匀速圆周运动时.由于通常情况下,重力和电场力为恒力,故不能充当向心力,所以一般情况下是重力恰好与电场力相平衡,洛伦兹力是以上力的合力.
③当带电粒子受的合力大小、方向均不断变化时,粒子做非匀变速曲线运动.
复合场:即在同一区域内同时有电场、磁场和重力场,此类问题看似简单,受力也不复杂,但仔细分析其运动往往比较难以把握.
带电粒子在复合场中运动的分析方法和一般思路:
①当带电粒子所受合外力为零时,将做匀速直线运动或处于静止状态.合外力恒定且与初速同向时做匀变速直线运动,常见的情况有:
Ⅰ、洛伦兹力为零(即v∥B),重力与电场力平衡,做匀速直线运动;或重力与电场力的合力恒定,做匀变速运动.
Ⅱ、洛伦兹力f洛与重力和电场力的合力平衡,做匀速直线运动.
②带电粒子所受合外力做向心力,带电粒子做匀速圆周运动时.由于通常情况下,重力和电场力为恒力,故不能充当向心力,所以一般情况下是重力恰好与电场力相平衡,洛伦兹力是以上力的合力.
③当带电粒子受的合力大小、方向均不断变化时,粒子做非匀变速曲线运动.

练习册系列答案
相关题目
 (2012?湖南模拟)如图所示,第四象限内有互相正交的电场强度为E的匀强电场与磁感应强度为B1=0.25T的匀强磁场,第一象限的某个矩形区域内,有方向垂直纸面向里、磁感应强度为B:的匀强磁场,磁场的下边界与x轴重合.质量为m=
(2012?湖南模拟)如图所示,第四象限内有互相正交的电场强度为E的匀强电场与磁感应强度为B1=0.25T的匀强磁场,第一象限的某个矩形区域内,有方向垂直纸面向里、磁感应强度为B:的匀强磁场,磁场的下边界与x轴重合.质量为m= (2012?湖南模拟)如图所示,一直立的汽缸用一质量为m的活塞封闭一定量的理想气体,活塞横截面积为S,汽缸内壁光滑且缸壁是导热的.开始活塞被固定,打开固定螺栓K,活塞下落,经过足够长时间后,活塞停在B点,已知AB=h,大气压强为p0,重力加速度为g.
(2012?湖南模拟)如图所示,一直立的汽缸用一质量为m的活塞封闭一定量的理想气体,活塞横截面积为S,汽缸内壁光滑且缸壁是导热的.开始活塞被固定,打开固定螺栓K,活塞下落,经过足够长时间后,活塞停在B点,已知AB=h,大气压强为p0,重力加速度为g. (2012?湖南模拟)如图所示,ABC为竖直平面内的光滑绝缘轨道,其中AB为倾斜直轨道,BC为与AB相切的圆形轨道,并且圆形轨道处在匀强磁场中,磁场方向垂直纸面向里.质量相同的甲、乙、丙三个小球中,甲球带正电、乙球带负电、丙球不带电.现将三个小球在轨道AB上分别从不同高度处由静止释放,都恰好通过圆形轨道的最高点,则( )
(2012?湖南模拟)如图所示,ABC为竖直平面内的光滑绝缘轨道,其中AB为倾斜直轨道,BC为与AB相切的圆形轨道,并且圆形轨道处在匀强磁场中,磁场方向垂直纸面向里.质量相同的甲、乙、丙三个小球中,甲球带正电、乙球带负电、丙球不带电.现将三个小球在轨道AB上分别从不同高度处由静止释放,都恰好通过圆形轨道的最高点,则( ) (2012?湖南模拟)如图所示,大量氢原子处于能级n=4的激发态,当它们向各较低能级跃迁时,对于多种可能的跃迁,下面说法中正确的是( )
(2012?湖南模拟)如图所示,大量氢原子处于能级n=4的激发态,当它们向各较低能级跃迁时,对于多种可能的跃迁,下面说法中正确的是( )