题目内容
【题目】如图甲所示，竖直放置的直角三角形NMP(MP边水平)，∠NMP＝θ，MP中点处固定一电荷量为Q的正点电荷，MN是长为a的光滑绝缘杆，杆上穿有一带正电的小球(可视为点电荷)，小球自N点由静止释放，小球的重力势能和电势能随位置x(取M点处x＝0)的变化图象如图乙所示(图中E0、E1、E2为已知量)，重力加速度为g，设无限远处电势为零，M点所处的水平面为重力零势能面．
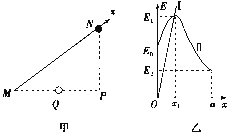
(1)图乙中表示电势能随位置变化的是哪条图线？
(2)求重力势能为E1时的横坐标x1和带电小球的质量m；
(3)求小球从N点运动到M点时的动能Ek.
【答案】(1)图线Ⅱ (2) 
, 
(3) 
【解析】试题分析：判断出电荷Q产生的电场分布，判断出正电荷下滑过程中电场力做功情况，即可判断出电势能的变化；由几何关系求出x1的位置，利用E1=mgh即可求的质量；在小球从N到M的过程中，利用动能定理求小球到达M点时的动能Ex。
(1)正Q电荷的电势分布规律是离它越近电势越高，带正电的小球的电势能为E＝qφ，可知正电荷从N点到M点的电势能先增大后减小，故图乙中表示电势能随位置变化的是图线Ⅱ.
(2)电势能为E1时，距M点的距离为
x1处重力势能E1＝mgx1sin θ
可得
(3)在小球从N点运动到M点的过程中，根据动能定理得：mgasin θ＋E2－E0＝Ek－0，
解得：
练习册系列答案
相关题目
